¿Cómo funciona chatGTP?

Ha llegado el tan esperado momento. Tras múltiples artículos explicando los fundamentos de redes neuronales ya hemos obtenido las bases necesarias para empezar a entender de manera definitiva y al detalle cómo se puede construir una herramienta como ChatGPT. Si bien ya sabemos bastante sobre el funcionamiento de redes neuronales, los grandes modelos de lenguaje combinan todos los conocimientos que hemos visto usando una lógica bastante abstracta e interesante.

En esta explicación iremos al grano y hablaremos de cómo funcionan los transformers. De hecho, el significado de GPT es “Generative Pre-trained Transformer”. Veremos el concepto de los transformers a lo largo de varios artículos. En este artículo hablaremos de vectores, tokens y embeddings. En futuros artículos hablaremos depositional embedding, mecanismos de atención, toda la arquitectura de los transformers y cómo escalar grandes modelos de lenguaje.

Además, a lo largo de este artículo entenderás por qué todo el mundo le da tanta importancia al número de parámetros de los modelos de lenguaje. Seguro que has escuchado alguna vez… ¡GPT-4 tendrá X veces más parámetros que GPT-3! ¿Impresionado? Bueno, para que algo te impresione de verdad, mejor entenderlo.

Vectores y tokens. La representación vectorial del vocabulario.

Si buscas por ahí la definición de un vector probablemente encuentres algo como que es una entidad matemática que “es una flecha” o una dirección o una línea en un espacio 2D o 3D… Y lo cierto es que sí, los vectores se utilizan para representar todo eso, pero para aplicar vectores en inteligencia artificial debemos utilizarlos para representar conceptos más complejos, abstractos e incluso dejar que las redes neuronales decidan darle la representación que quieran. Y con esto que te digo tengo un cierto dilema. Verás, explicar vectores desde un punto de vista geométrico es mucho más entendible y por ello lo haré así. Sólo te pido que a lo largo del artículo no te olvides de lo siguiente:

A continuación voy a graficar un ejemplo de un vector con los valores (3,4). Y entenderás por qué se dice que un vector puede representar una “flecha”, una dirección o una velocidad.

Pero antes de continuar explicando cómo se procesa el lenguaje natural en una red neuronal quiero terminar de explicar la base de los vectores. Para ello necesito que sepas qué es un vector normalizado.

Un vector normalizado es aquel que ha sido escalado de tal manera que su longitud o magnitud sea igual a 1, pero su dirección permanece igual. La normalización de un vector es un proceso que nos permite comparar y trabajar con vectores de diferentes magnitudes en términos de dirección. Esto es útil en muchos contextos, como en el análisis de datos y en el procesamiento de señales, donde la dirección de un vector es más importante que su magnitud.

Para normalizar un vector, dividimos cada componente del vector por su magnitud. La magnitud de un vector se calcula como la raíz cuadrada de la suma de los cuadrados de sus componentes.

A continuación te muestro un ejemplo de un vector no normalizado y su versión normalizada:

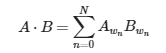
Embedding y tokenización: El proceso de “traducir” de palabra a vector.

¡Genial! Ya hemos entendido todo lo necesario para que una red neuronal nos entienda. Los grandes modelos de lenguaje, dicho de forma muy reduccionista son “simplemente” redes neuronales que reciben una secuencia de tokens como input y como output generan un vector donde cada valor número representa la probabilidad de que un determinado token sea la siguiente. Así es como escriben, y como entrenan. Tú te creas una red neuronal que reciba unos tokens (cada token siendo un vector que representa las características de una palabra). La red escupe el token más probable y de ahí generas la función de coste y haces backpropagation hasta que sepa completar textos. Pues aunque realmente es más complejo, la idea va por ese camino.

Ahora bien… ¿Cómo podemos hacer para pasar de una palabra a un token? ¿Voy a tener que puntuar miles de característica por cada palabra? ¿Y con las mayúsculas y minúsculas? Menuda faena…

No te preocupes, la clave está en delegar esta tarea a una red neuronal.

Imagina que estamos trabajando con un modelo de lenguaje muy primitivo que solamente sabe expresarse con 5 palabras. Estas palabras son: “gustar”, “mi”, “no”, “cosa”, “hacer”.

Con esto ya podríamos generar frases con un mínimo de sentido. “Mi gustar cosa”, “Mi no gustar hacer cosa”… Muy primitivo pero ideal para una explicación.

Representaremos cada palabra con un vector categórico. Un vector categórico es un vector donde cada posición indica si el vector representa un elemento o no. Si lo representa, ese valor será 1 y si no 0. En el contexto de palabras, cada vector tendrá tantos números como palabras existan en el vocabulario. Y todos los valores serán 0 excepto 1.

Por ejemplo podemos realizar la siguiente asignación de vectores:

• La palabra “gustar” será el vector (1,0,0,0,0).
• La palabra “mi” será el vector (0,1,0,0,0).
• La palabra “cosa” será el vector (0,0,1,0,0).
• La palabra “hacer” será el vector (0,0,0,1,0).
• La palabra “no” será el vector (0,0,0,0,1).

Generar algorítmicamente esta asociación es muy sencillo, y ahora podríamos usar ese vector como capa de input de nuestra red neuronal. Donde hay 5 neuronas y si la red neuronal recibe como input la palabra “gustar”, la primera neurona recibirá como valor 1 y el resto 0.

Genial, ¡Ya sabemos cómo enviar palabras a la red neurona! Pero recuerda que la finalidad de esta red neuronal no es en sí predecir el siguiente token, sino obtener un token enriquecido con propiedades de cada palabra. Por ejemplo, imagina que el output de la red como output tiene el vector de 3 dimensiones que utilizamos anteriormente para definir formalidad, positividad y frecuencia de las palabras. Bien, pues generalmente el output de esta red neuronal serán vectores de miles de dimensiones para convertir palabras representadas con tokens como “(1,0,0,0,0)” que no contienen información del significado de la palabra a tokens ricos en información.

Es de esta manera en la que cuando una red neuronal “oye” una palabra, entiende su significado y no es una secuencia aleatoria de caracteres.

Muy bien, pero todavía nos quedan algunas incógnitas por resolver… ¿Cómo entrenamos a esta red? ¿Cómo definimos las propiedades de cada palabra en el output? El output de esta red estará conectado al input de la red neuronal que sí pretende predecir el siguiente token de modo que al aplicar el backpropagation también en esta red, será el propio proceso de aprendizaje el que determine con la detección de patrones qué propiedades expresarán los tokens enriquecidos.

Para dar un poco de vocabulario técnico, los vectores tipo “(1,0,0,0,0)” se llaman tokens one-hot encoding. Y el proceso de transformar información en con datos redundantes a información relevante y condensada se le conoce como embedding. Por ello el proceso de convertir el vector “(1,0,0,0,0)” en el vector “(90% positivo, 50% formal, 99% frecuente)” se conoce como embedding. Hay más tipos de embeddings pero esos los conoceremos más adelante.

Y así es como GPT aprende palabras. Para él las palabras no son formadas por letras sino por propiedades que él mismo ha definido intentando predecir tokens. Es importante mencionar que realmente los tokens son secuencias de caracteres que no son exactamente las palabras de nuestro lenguaje.

Las palabras muchas veces tienen elementos en común. Por ejemplo, el plural de monstruo es “monstruo” + la letra “s”. Un token realmente se asemeja más a una sílaba que a una palabra. ¿Y por qué? Bueno, pues porque así gpt puede encontrar patrones más complejos en el lenguaje y tiene mejor rendimiento. En toda mi explicación me he referido a tokens como representaciones de una palabra completa únicamente para simplificar la explicación.

¡Este es un gran paso para entender el funcionamiento de los transformers! Aunque aún nos queda mucho recorrido por delante. Voy a marcar en el esquema de arquitectura de los transformers lo que hemos aprendido hoy:

Para terminar con una conclusión didáctica, supongo que ahora entenderás por qué todo el mundo compara los diferentes modelos de lenguaje por la cantidad de parámetros. A más parámetros, mayor capacidad de vocabulario, mayor número de propiedades al realizar el embedding del input y por tanto mayor número de patrones a analizar por parte de la red. A más patrones a detectar, puedes tener una red más grande sin overfitting y por tanto más inteligente. De ahí que todo el mundo mida las predicciones de las capacidades de los nuevos modelos de lenguaje en función de su cantidad de parámetros.

¡Enhorabuena! Ya has ganado la primera batalla para comprender a los transformers. ¡Que continue la conquista!