En los últimos artículos hemos comentado todos los aspectos conceptuales importantes sobre redes neuronales. Pero todavía nos queda en el tintero algunas cosas importantes y algunas incógnitas por resolver. Sí, vale, ya entiendo cómo funcionan las redes neuronales. Pero… ¿Con qué criterio escojo las propiedades de mis redes neuronales? ¿Cómo puedo entrenar redes neuronales con millones de datos como hacen las grandes compañías?
En este artículo lo aprenderemos y haremos un ejemplo en código de un clasificador de imágenes aprendiendo también el concepto de red neuronal convolucional. Como todo lo que voy a explicar son conceptos muy independientes, en esta ocasión adoptaré un formato un poco diferente y primero le daré más relevancia a lo teórico. Luego, nos pondremos manos a la obra con nuestro modelo.
Antes de nada si te has perdido los episodios anteriores aquí te dejamos los enlaces:
Capítulo 1 – Tutorial inteligencia artificial
Capítulo 2 – Entendiendo las Redes Neuronales
Capítulo 3 – Uso de la Matrices para las Redes Neuronales
Capítulo 4 –¿Qué es el overfitting?
¿Listo? ¡Vamos a por ello!
[powerkit_toc title=»Table of Contents» depth=»2″ min_count=»1″ min_characters=»1000″ btn_hide=»false» default_state=»expanded»]
Entrenando Modelos Gigantes de Deep Learning: Descubre el Poder de los Data Generators
¿Alguna vez te has preguntado cómo se entrenan modelos de deep learning con millones de datos si éstos no caben en nuestros ordenadores? Si has estado investigando el mundo del deep learning, es probable que hayas encontrado este problema. La memoria RAM de nuestros sistemas, aunque cada vez más grande, sigue siendo limitada, y muchos conjuntos de datos superan ampliamente estas capacidades.
Aquí es donde entra en juego el concepto de data generators o generadores de datos. Pero, ¿qué son exactamente y cómo nos ayudan a entrenar modelos gigantes?
Los data generators son una solución inteligente para el problema de la falta de memoria RAM. En lugar de cargar todo el conjunto de datos en la memoria, los data generators leen y procesan los datos en pequeños lotes o batches. Esto permite a nuestros modelos trabajar con datos mucho más grandes de lo que podría caber en nuestra memoria RAM.
Bien, ¿Y cómo Funcionan los Data Generators? El proceso es bastante simple. Los data generators leen una parte del conjunto de datos (un batch) desde el almacenamiento, la procesan y la envían al modelo para el entrenamiento. Una vez que se completa el entrenamiento con ese lote, el data generator lee el siguiente lote y repite el proceso. De esta manera, el modelo puede entrenarse con todo el conjunto de datos sin la necesidad de cargarlo completamente en la memoria.
Beneficios de Usar Data Generators
Además de permitirnos trabajar con conjuntos de datos más grandes de lo que la memoria RAM puede soportar, los data generators también tienen otros beneficios, como:
Eficiencia: Al trabajar con lotes, se reduce la sobrecarga de la memoria y se optimiza la utilización de los recursos del sistema.
Flexibilidad: Los data generators se pueden adaptar fácilmente a diferentes formatos de datos y procesos de preprocesamiento.
Aumentación de datos: Los data generators también pueden aplicar técnicas de aumentación de datos en tiempo real, lo que ayuda a mejorar el rendimiento y la generalización del modelo.
Criterios para diseñar una red neuronal
Antes de empezar te advierto que para varios aspectos te encontrarás que no hay un criterio definido para definir varias características de nuestra red neuronal más que intuición y experiencia. Al final de éste apartado te mostraré una forma profesional de buscar algorítmicamente los valores más eficientes de todas esas características.
Cuando se trata de diseñar la estructura de una red neuronal, hay varias decisiones que debemos tomar, desde la cantidad de capas y neuronas hasta los optimizadores y funciones de coste. Con tantas opciones disponibles, ¿cómo podemos tomar las decisiones correctas? ¡Que alguien llame a un senior!
1. Determina la cantidad de capas y neuronas (y su función de activación)
La cantidad de capas y neuronas en cada capa puede afectar significativamente el rendimiento de tu red neuronal. Aquí hay algunas pautas para ayudarte a decidir:
- Capa de entrada: Aquí no hay mucho que discutir: El número de neuronas en la capa de entrada debe coincidir con el número de características de entrada en tus datos. Pero ten en cuenta que cuanto más sencilla sea la entrada sin perder información más fácil será que tu red aprenda. Si por ejemplo trabajas con imágenes, considera reducir su resolución a un punto donde la información relevante no se pierda.
- Capas ocultas: No hay una regla única para determinar la cantidad de capas ocultas y neuronas. Sin embargo, en general, más capas pueden ayudar a aprender patrones más complejos, pero también pueden aumentar el riesgo de overfitting y el tiempo de entrenamiento. Prueba con diferentes configuraciones y elige la que mejor funcione para tu problema. (Luego vemos una forma más interesante de enfocar esto)
- Capa de ouptut: El número de neuronas en la capa de salida depende del tipo de problema y sobre todo de la solución que quieres que tu modelo ofrezca. Para clasificación binaria, necesitas una única neurona, mientras que para clasificación multiclase, necesitas tantas neuronas como clases. Para problemas de regresión, una única neurona es suficiente.
Funciones de activación
Las funciones de activación son un componente crucial, ya que introducen no linealidades en el modelo, permitiendo que las redes aprendan patrones más complejos. Pero claro, esa no-linealidad tiene un comportamiento muy distinto entre cada función de activación. Elegir la función de activación adecuada para cada capa de la red es esencial para garantizar un buen rendimiento. A continuación, se presentan algunos criterios para elegir funciones de activación según el tipo de capa:
Capa de entrada
En general, no se aplican funciones de activación en la capa de entrada, ya que los datos de entrada suelen ser valores en bruto o características previamente procesadas. Sin embargo, sí es importante preprocesar los datos de entrada.
El preprocesamiento de datos es un paso esencial en el proceso de construcción de modelos de aprendizaje automático y profundo, ya que ayuda a mejorar la calidad de los datos y, por lo tanto, el rendimiento del modelo. Algunas razones por las que el preprocesamiento de datos es importante incluyen:
- Eliminación de ruido y valores atípicos
- Manejo de datos faltantes
- Transformación de variables categóricas en variables numéricas
- Mejora de la eficiencia computacional
- Facilita la convergencia de algoritmos de optimización
Feature Scaling (Escalado de características) es una técnica de preprocesamiento que se utiliza para garantizar que todas las características tengan la misma escala o rango, lo que facilita la comparación y la interpretación de las características. En muchos algoritmos de aprendizaje automático y profundo, el escalado de características es esencial para garantizar la convergencia rápida y un rendimiento óptimo.
Existen diferentes técnicas. Las más usuales son:
Normalización (Min-Max Scaling): Transforma las características al rango [0, 1] ajustando cada característica según sus valores mínimo y máximo.
x norm= x – x(min) / x(max) – x(min)
Estandarización (Z-score Scaling): Transforma las características para que tengan media 0 y desviación estándar 1, eliminando la unidad de medida y permitiendo comparar características con diferentes escalas y distribuciones.
x std= x – μ / σ
Escalado robusto (Robust Scaling): Utiliza la mediana y el rango intercuartil para escalar las características, lo que lo hace más resistente a los valores atípicos en comparación con la normalización y la estandarización.
x robust = x – Q1 / Q3 – Q1
Ejemplo:
Supongamos que se te pide establecer una relación entre la edad de las personas y su salario anual con la intención de compra. En este caso, la edad y el salario anual tienen diferentes escalas: la edad varía típicamente entre 0 y 100 años, mientras que el salario anual puede variar desde unos miles hasta varios millones. Si no se escalan las características, el salario anual dominará la relación debido a su mayor magnitud y la edad no tendrá tanto peso en el modelo.
Para evitar esto, puedes aplicar una técnica de escalado de características, como la estandarización. Al hacerlo, la edad y el salario anual se transformarán para que tengan una media de 0 y una desviación estándar de 1, lo que permitirá al algoritmo de aprendizaje automático considerar adecuadamente la importancia de ambas características al predecir la intención de compra.
Para desarrollar un criterio que nos permita afrontar éste desafío recomiendo estudiar ciencia de datos y realizar ejercicios.
Capas ocultas
Para las capas ocultas, hay varias opciones de funciones de activación, y elegir la adecuada dependerá del problema y del tipo de datos:
- ReLU (Rectified Linear Unit): Es la función de activación más comúnmente utilizada en las capas ocultas debido a su simplicidad y eficiencia computacional. Funciona bien en la mayoría de los casos, pero puede sufrir del problema de «neuronas muertas» si la salida de la activación es siempre negativa.
- Leaky ReLU y Parametric ReLU (PReLU): Son variantes de la ReLU que resuelven el problema de las neuronas muertas al permitir valores negativos pequeños en la salida. Pueden ser útiles en casos donde las ReLU estándar no funcionan bien.
- Sigmoid: Fue popular en el pasado, pero ahora se usa con menos frecuencia en las capas ocultas debido a problemas como el desvanecimiento del gradiente y la saturación. Sin embargo, sigue siendo útil en ciertos casos, como en modelos de redes neuronales recurrentes (RNN) y en problemas de clasificación binaria.
- Tangente hiperbólica (tanh): Es similar a la función sigmoidal, pero varía entre -1 y 1 en lugar de 0 y 1. Al igual que la sigmoidal, puede sufrir de desvanecimiento del gradiente, pero aún se usa en algunos casos, como en las RNN.
- Swish, ELU y otras funciones de activación avanzadas: Existen varias funciones de activación más avanzadas que pueden ofrecer mejoras en la convergencia y el rendimiento del modelo. Si las funciones de activación tradicionales no ofrecen buenos resultados, podrías experimentar con estas funciones más avanzadas.
Capa de output
La elección de la función de activación en la capa de salida depende del tipo de problema y de la tarea que estés resolviendo:
- Regresión: En general, no se aplica ninguna función de activación «diferente» para transformar los datos en problemas de regresión, ya que se busca una salida continua en un rango no acotado. Sin embargo, si necesitas restringir el rango de la salida, podrías usar funciones de activación como ReLU, sigmoid o tanh.
- Cuando tu tarea es clasificar algo en dos categorías (como detectar si un correo es spam o no), típicamente se utiliza la función sigmoide. Esta función convierte los números de entrada en probabilidades que suman 1, lo que es muy útil para representar la probabilidad de que una entrada pertenezca a una de las dos clases.
- Clasificación multiclase: Si estás en el negocio de clasificar cosas en más de dos categorías (como clasificar imágenes de dígitos escritos a mano), la función softmax es la que sueles querer. Similar a la sigmoide, convierte los números de entrada en probabilidades. Pero en este caso, te da un conjunto de probabilidades que suman 1 para todas las posibles clases.
2. Elige el tipo de función de coste y el optimizador
La función de coste y el optimizador son componentes críticos en el entrenamiento de una red neuronal. Algunas pautas para elegirlos son:
Función de coste
Elegir función de coste suele ser cuestión de experiencia y en función del tipo de problema a resolver. De todas las funciones que existen, las hay idóneas para un tipo de problema. Y la lógica para elegirlas suele ser mirar una tabla. Tipo, «Para problemas de clasificación, utiliza funciones como la entropía cruzada. Para problemas de regresión, el error cuadrático medio es una opción popular…»
Te dejo una tabla bastante completa recatada de mis apuntes:
- Error cuadrático medio (MSE – Mean Squared Error): Es una función de costo comúnmente utilizada para problemas de regresión. Calcula el promedio de los cuadrados de las diferencias entre las predicciones y los valores verdaderos.
- Error absoluto medio (MAE – Mean Absolute Error): Similar al MSE, pero en lugar de calcular el promedio de los cuadrados de las diferencias, calcula el promedio de los valores absolutos de las diferencias. También se usa principalmente en problemas de regresión.
- Entropía cruzada binaria (Binary Cross-Entropy): Se utiliza en problemas de clasificación binaria. Mide la discrepancia entre las etiquetas verdaderas y las predicciones probabilísticas del modelo.
- Entropía cruzada categórica (Categorical Cross-Entropy): Se utiliza en problemas de clasificación multiclase. Mide la discrepancia entre las etiquetas verdaderas codificadas en one-hot y las predicciones probabilísticas del modelo para cada clase.
- Entropía cruzada escasa (Sparse Categorical Cross-Entropy): Es similar a la entropía cruzada categórica, pero se utiliza cuando las etiquetas verdaderas son enteros en lugar de codificación one-hot.
- Hinge Loss: Se utiliza en máquinas de vectores de soporte (SVM) y en algunas redes neuronales para problemas de clasificación. Busca maximizar el margen entre las clases.
- Huber Loss: Es una combinación de MSE y MAE y es menos sensible a los valores atípicos en comparación con el MSE. Se utiliza en problemas de regresión.
- Pérdida logarítmica (Log Loss): Mide el rendimiento de un modelo de clasificación en el que la entrada de predicción es una probabilidad de pertenecer a una clase específica.
- Pérdida de Kullback-Leibler Divergence (KL Divergence): Mide la diferencia entre dos distribuciones de probabilidad. Se utiliza en problemas de regresión y clasificación cuando se busca minimizar la discrepancia entre las distribuciones de probabilidad verdaderas y las predichas por el modelo.
- Pérdida de Cosine Similarity: Mide la similitud entre dos vectores al calcular el coseno del ángulo entre ellos. Se puede utilizar en problemas de clasificación y regresión.
- Pérdida de Poisson: Mide la discrepancia entre las predicciones y los valores verdaderos en función de la distribución de Poisson. Se utiliza en problemas de regresión.
Optimizador
Como vimos en el anterior post, Adam suele ser la que tiene mejor rendimiento pero hay que tener en cuenta que continuamente se están descubriendo nuevos optimizadores y esto puede quedar obsoleto. Elegir optimizador es cuestión de estar al día de las noticias de Deep Learning.
3. Configura el porcentaje de dropout, regularización y learning rate
Estos parámetros pueden ayudar a prevenir el sobreajuste y mejorar el rendimiento del modelo:
- Dropout: Utiliza dropout en las capas ocultas para evitar la «coadaptación» que comentamos en el artículo del overfitting. Los valores típicos varían entre 0.2 y 0.5 y no hay un criterio fijo.
- Learning rate: Elige un learning rate que permita una convergencia estable y rápida. Prueba con diferentes valores y monitorea el progreso del entrenamiento. Pero bueno, con la propiedad adaptativa del learning rate en el uso de optimizadores como Adam pese a ser cuestión de try and error suele no dar dolor de cabeza.
- Regularización: La elección entre regularización L1 y L2 en redes neuronales depende del problema a resolver. L1 genera soluciones dispersas, favoreciendo modelos más interpretables y seleccionando características importantes, mientras que L2 reduce suavemente los coeficientes para modelos más equilibrados. Si se esperan pocas características importantes, se puede usar L1; si se cree que todas son relevantes, se puede optar por L2. También se puede utilizar «Elastic Net», que combina L1 y L2.
4. Establece la duración del entrenamiento o criterios de early stopping
- Duración del entrenamiento: Puedes establecer un número fijo de épocas para el entrenamiento. Sin embargo, esto puede resultar en underfitting o overfitting. Lo mejor es aplicar un criterio para parar el entrenamiento cuando el modelo no mejora sus resultados. (veremos esto más abajo)
El Arte de encontrar la Combinación Idónea: Automatiza el Proceso con KerasTuner
Encontrar la combinación perfecta de ajustes para todos los parámetros mencionados en la sección anterior puede ser un proceso complicado y lleno de prueba y error. Afortunadamente, existen herramientas como KerasTuner que pueden facilitar esta tarea al automatizar el proceso de búsqueda de la configuración óptima para tu red neuronal.
Nosotros usaremos KerasTuner. Se trata de una biblioteca de Python para ajuste de hiperparámetros en modelos de aprendizaje profundo creados con Keras (que es parte de TensorFlow). Esta herramienta simplifica el proceso de encontrar la combinación idónea de hiperparámetros al realizar búsquedas automatizadas y eficientes.
La idea es definir un espacio de búsqueda para los hiperparámetros que deseas optimizar, como la cantidad de capas ocultas, el número de neuronas, la tasa de aprendizaje, el optimizador, entre otros. Luego, KerasTuner evalúa diferentes combinaciones de estos hiperparámetros y encuentra la configuración que produce el mejor rendimiento en función de una métrica de validación predefinida.
Aplicando todo lo aprendido con Tensorflow y Keras programando una CNN
¿Alguna vez te has preguntado cómo es posible que aplicaciones como Facebook o Google Fotos puedan reconocer a tus amigos en las fotos que subes? ¡La respuesta está en las redes neuronales convolucionales (CNN)! Sigue leyendo y descubre cómo estas asombrosas arquitecturas de deep learning están revolucionando el mundo de la clasificación de imágenes.
Estructura de una CNN
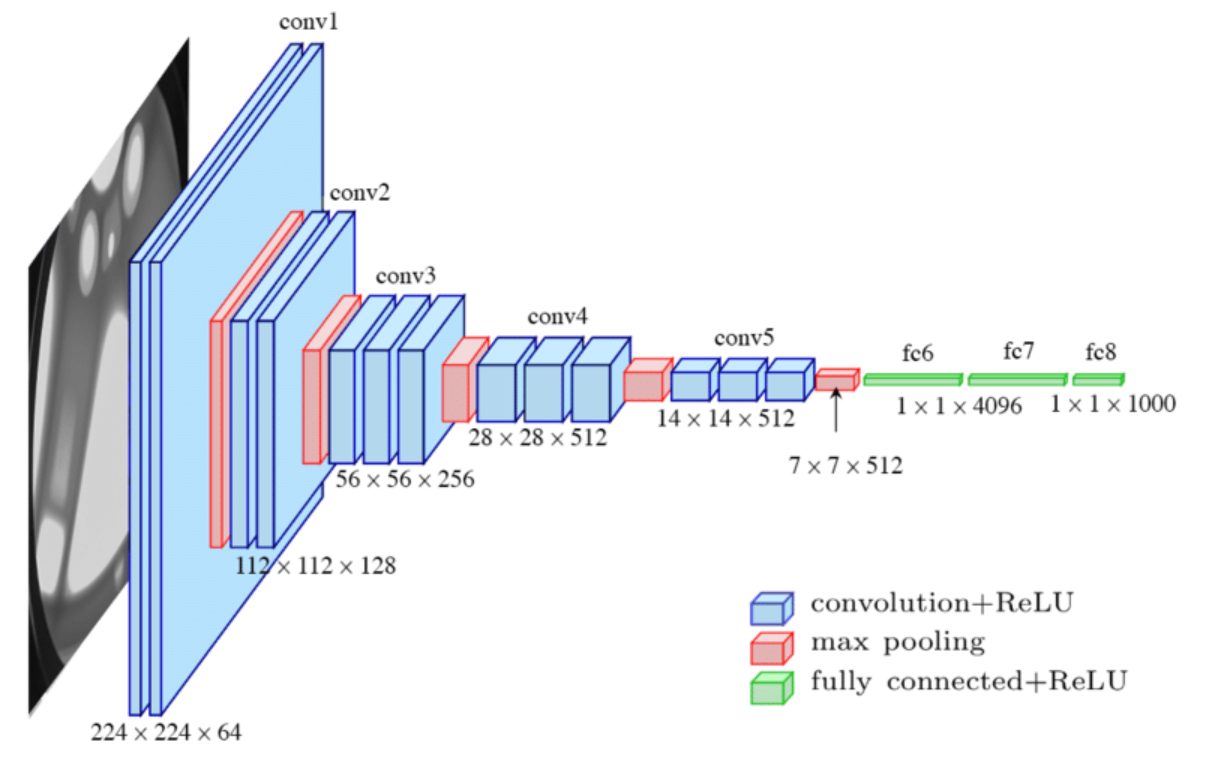
Imagina que quieres que una red neuronal detecte los patrones para detectar si una foto de un carácter escrito a mano es un dígito entre 0 y 9. Probablemente pienses, «oh claro, la red neuronal buscará patrones de formas a través de píxeles contiguos». Por ejemplo, un «8» son 2 círculos posicionados uno encima del otro. Un «1» es un palo o un palo cuya parte superior tiene un palito pequeño en diagonal y la parte inferior puede tener un palito pequeño perpendicular.
Ejemplo para el dígito 8
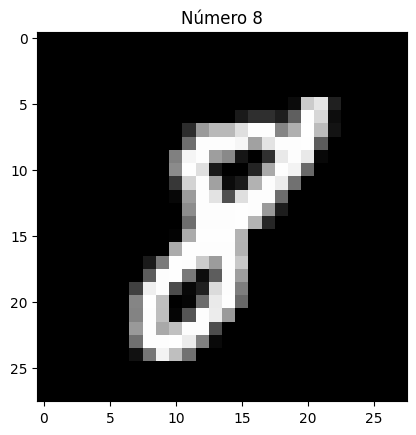
Entendiendo los kernel
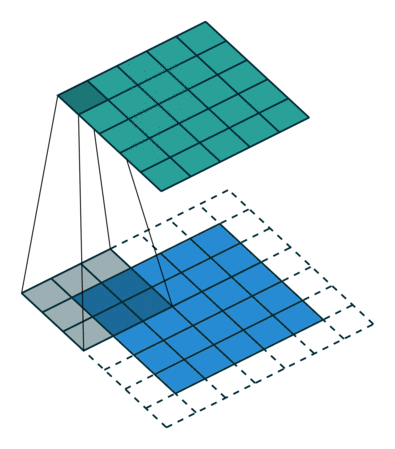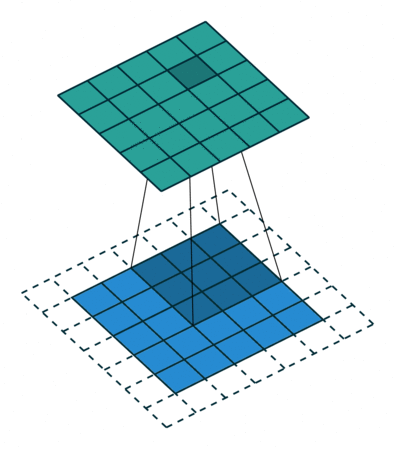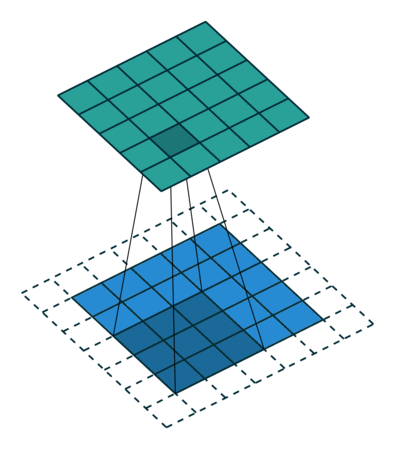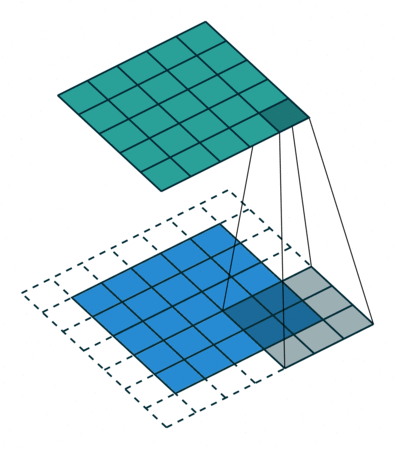
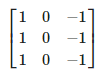
Este kernel nos puede servir para detectar bordes verticales. Piénsalo, si NO hay un cambio de color en los píxeles de la izquierda respecto a los de la derecha, dado que los de la derecha se quedan igual (se multiplican por 1) y los de la derecha cambian de signo (se multiplican por -1), se cancelarán. Ahora bien, si tienen valores diferentes (hay un cambio de color en vertical) el resultado será mayor. Razón por la que podemos buscar formas de tener kernels para detección de bordes.
Por ejemplo, aquí tendríamos un kernel para detección de bordes horizontales:
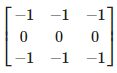
import cv2import numpy as npimport matplotlib.pyplot as pltfrom scipy.signal import convolve2dimport requestsfrom PIL import Imagefrom io import BytesIO# Descarga una imagen del dataset Caltech101image_url = «https://img.huffingtonpost.es/files/main_image_720_480/uploads/2023/04/21/elon-musk-en-la-alfombra-de-la-met-gala-de-2022.jpeg»response = requests.get(image_url)img = Image.open(BytesIO(response.content))# Convierte la imagen a escala de grises y a un array de NumPyimg_gray = img.convert(‘L’)img_gray_np = np.array(img_gray)# Define un kernel para la detección de bordeskernel = np.array([[1, 0, -1],[1, 0,-1],[1, 0, -1]])# Aplica el kernel a la imagen utilizando convolución 2Dimg_edges = convolve2d(img_gray_np, kernel, mode=’same’)# Aplica el umbral a la imagen de bordesthreshold = 50img_edges[img_edges > threshold] = 255img_edges[img_edges <= threshold] = 0# Muestra la imagen original y la imagen con bordes detectadosfig, axes = plt.subplots(1, 2, figsize=(10, 5))axes[0].imshow(img)axes[0].set_title(‘Imagen original’)axes[1].imshow(img_edges, cmap=’gray’)axes[1].set_title(‘Imagen con bordes detectados’)plt.show()
img_gray = img.convert(‘L’)
img_gray_np = np.array(img_gray)# Define un kernel para la detección de bordes
kernel = np.array([[1, 1, 1],
[0, 0,0],
[-1, -1, -1]])# Aplica el kernel a la imagen utilizando convolución 2D
img_edges = convolve2d(img_gray_np, kernel, mode=’same’)# Aplica el umbral a la imagen de bordes
threshold = 50
img_edges[img_edges > threshold] = 255
img_edges[img_edges <= threshold] = 0# Muestra la imagen original y la imagen con bordes detectados
fig, axes = plt.subplots(1, 2, figsize=(10, 5))axes[0].imshow(img)
axes[0].set_title(‘Imagen original’)axes[1].imshow(img_edges, cmap=’gray’)
axes[1].set_title(‘Imagen con bordes detectados’)plt.show()
Ejemplo con otros kernels de detección de bordes
img_gray = img.convert(‘L’)
img_gray_np = np.array(img_gray)# Define un kernel para la detección de bordes
kernel = np.array([[-1, -1, -1],
[-1, 8,-1],
[-1, -1, -1]])# Aplica el kernel a la imagen utilizando convolución 2D
img_edges = convolve2d(img_gray_np, kernel, mode=’same’)# Aplica el umbral a la imagen de bordes
threshold = 50
img_edges[img_edges > threshold] = 255
img_edges[img_edges <= threshold] = 0# Muestra la imagen original y la imagen con bordes detectados
fig, axes = plt.subplots(1, 2, figsize=(10, 5))axes[0].imshow(img)
axes[0].set_title(‘Imagen original’)axes[1].imshow(img_edges, cmap=’gray’)
axes[1].set_title(‘Imagen con bordes detectados’)plt.show()
Como ya te habrás imaginado, para una red neuronal es mucho más fácil detectar patrones de formas con ésta información que sin ella. Por ello, la detección de bordes es algo fundamental para detectar patrones de formas en imágenes. Aunque realmente los kernels de las CNNs se crean con valores aleatorios y es el entrenamiento de la red el que los va definiendo.
Teniendo en cuenta que las imágenes tienen tres datos por píxel (intensidad del color rojo, verde y azul) las convoluciones también sirven para detectar patrones relacionados con colores. O patrones de colores y formas combinados.
A este proceso de aplicar kernels a una imagen se le conoce como capas de convolución. Existen formas más avanzadas de trabajar con kernels y si quieres buscar más información te recomiendo que te informes acerca de el padding y los strides de un Kernel.
Cada capa de convolución aplica más de un kernel para tratar de detectar tipos de patrones diferentes. ¿Problema? Pues cada vez que aplicas una convolución obtienes más información ya que, por ejemplo, pasas de tener una sola imagen a una imagen con los bordes verticales y otra con las horizontales. Mientras antes ibas a usar como parámetro de tu red una sola imagen ahora son 2. De forma que conforme más convoluciones apliques más lenta será tu red. Precisamente comentamos que las redes clásicas son malas posicionando patrones en imágenes grandes…
Para solucionar éste problema se usan las capas de Pooling. Existen varios tipos pero principalmente se usa MaxPooling ya que es la que generalmente da mejor resultado. Funciona como la capa de convolución solo que en lugar de realizar la operación de convolución matricial lo que hace es quedarse solamente con el valor máximo.
GIF ilustrativo:
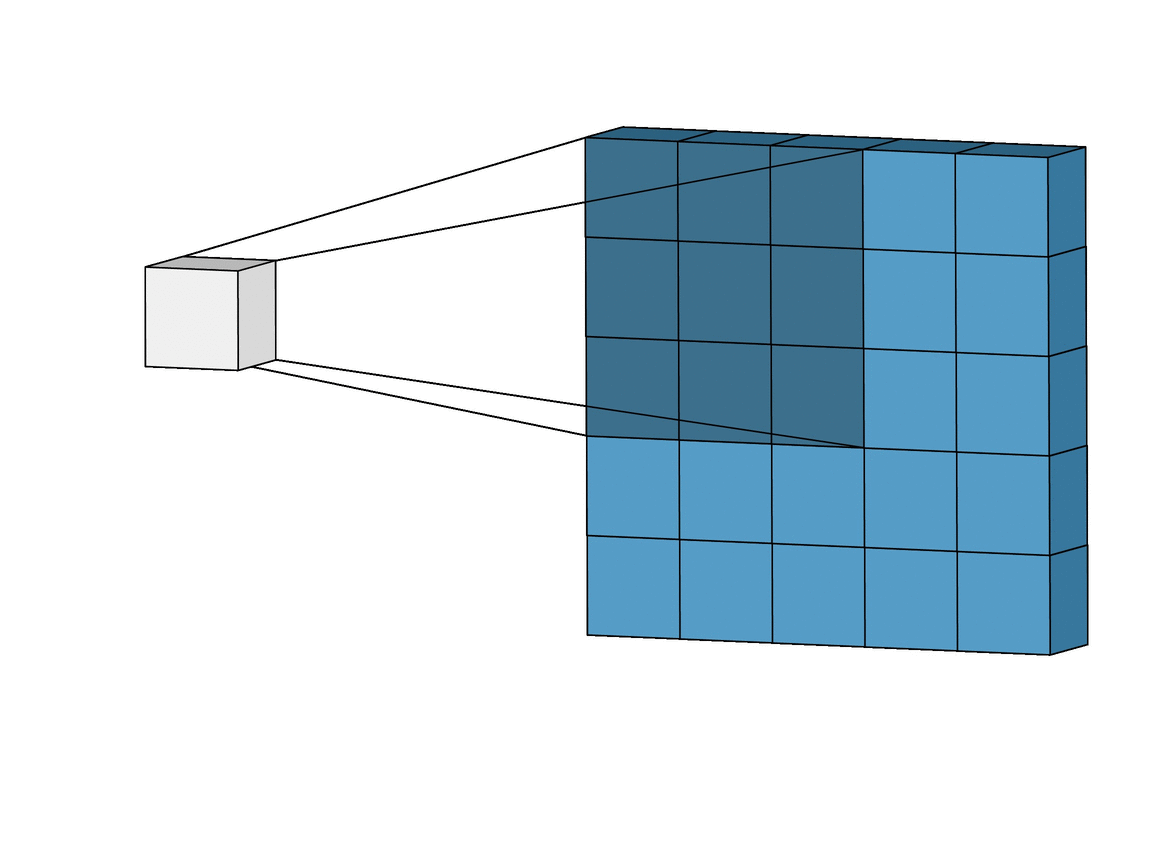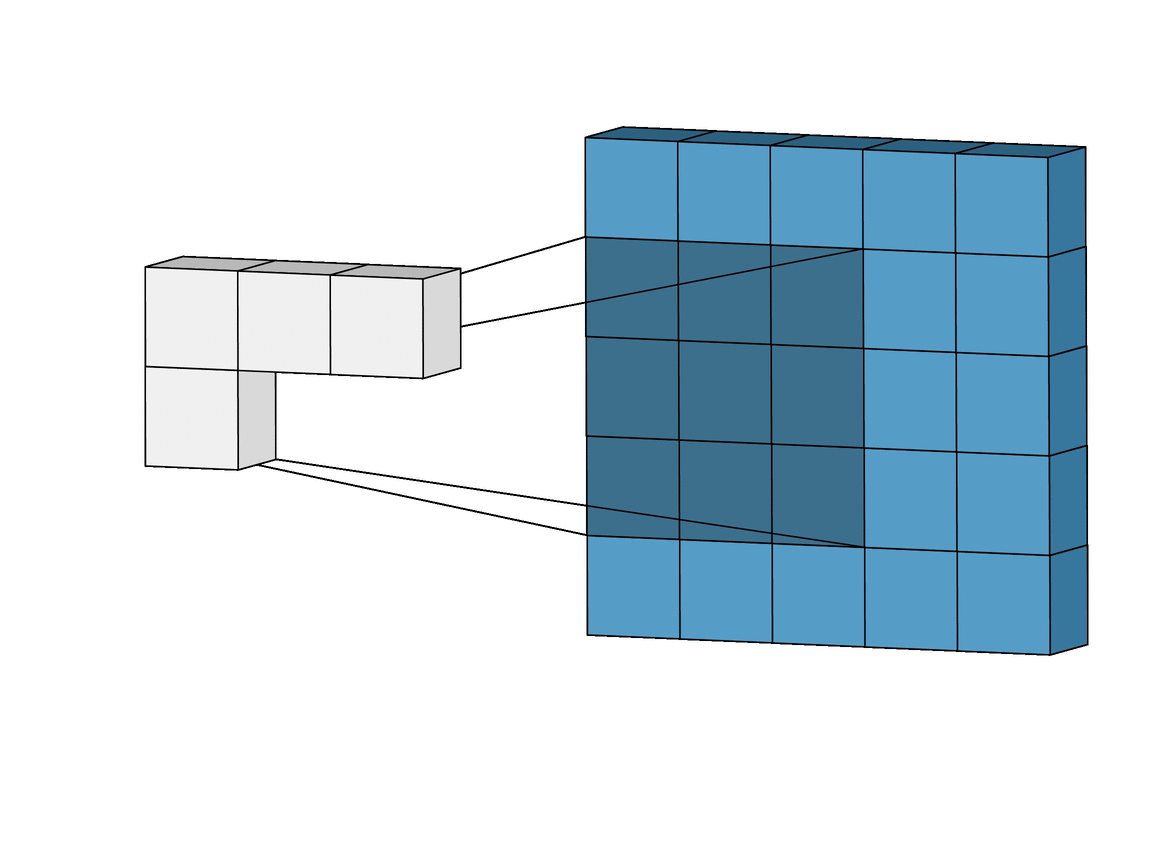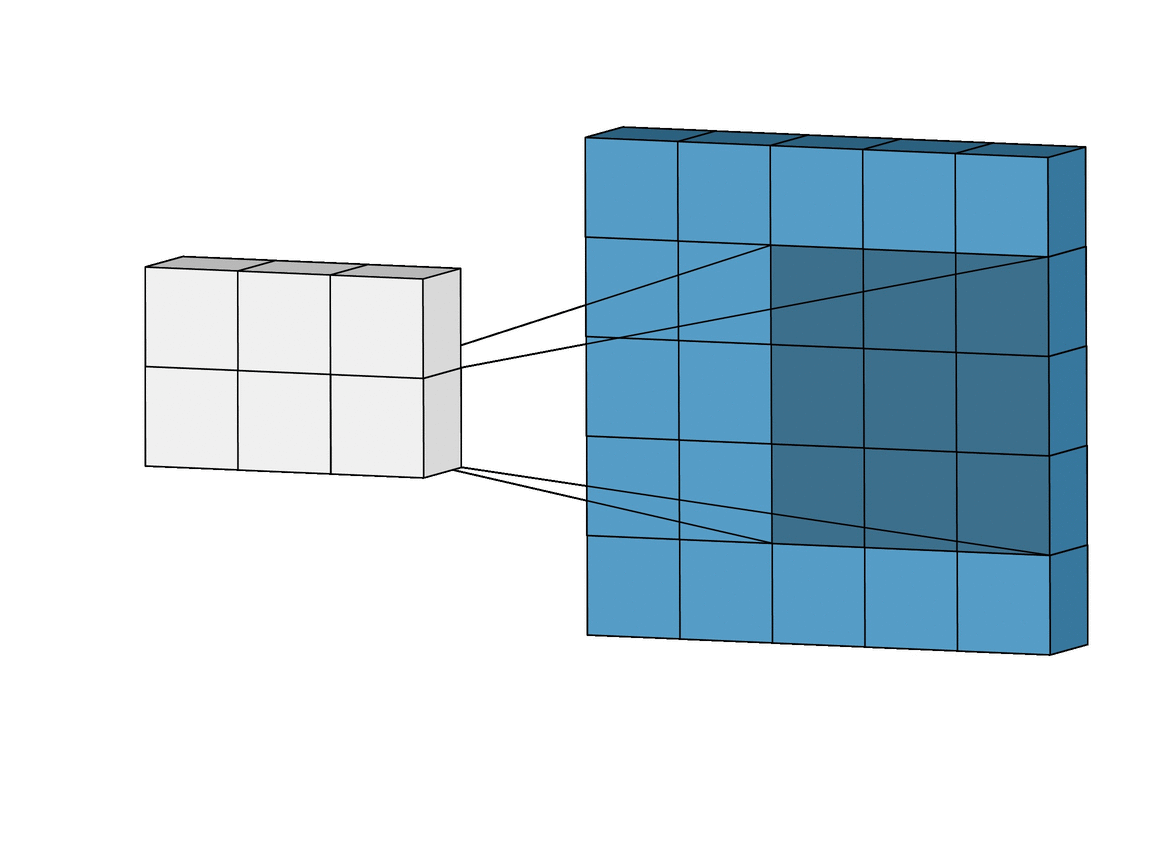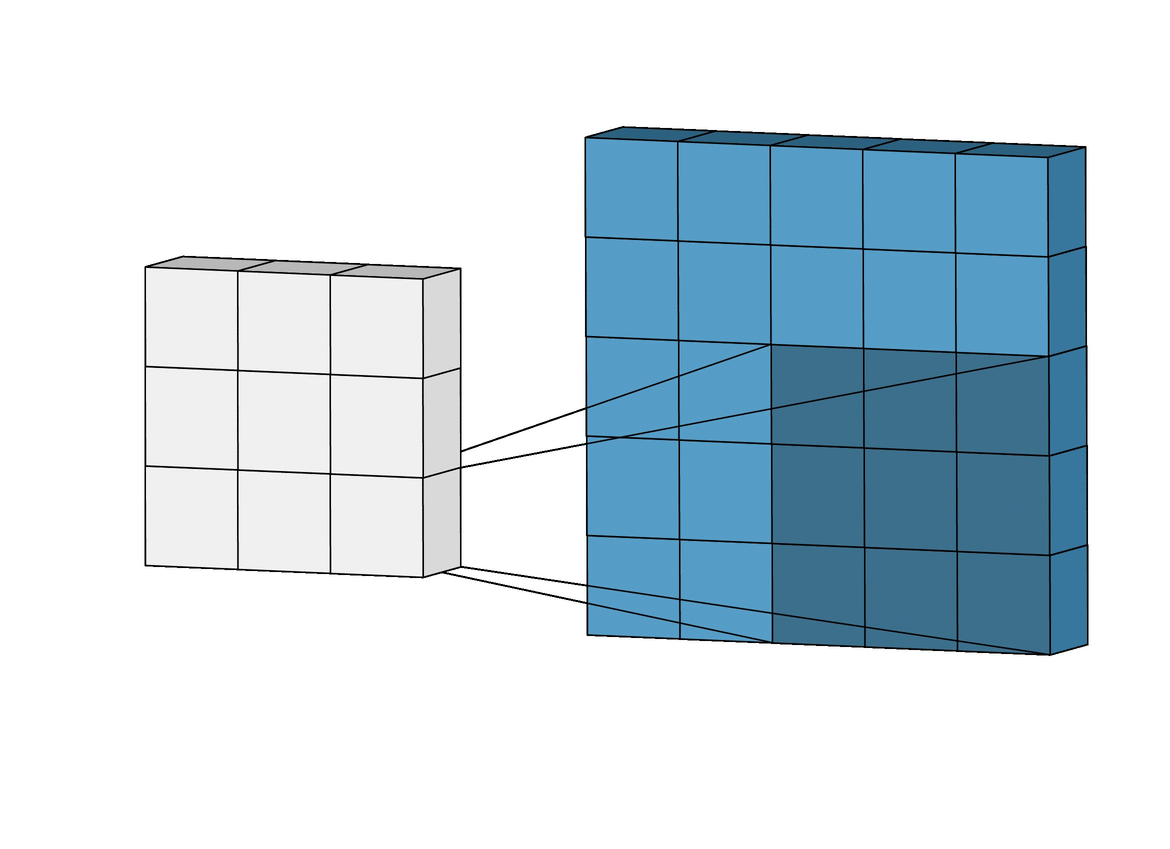
Las capas de Pooling solucionan nuestros dos principales problemas:
Por un lado generan un output más pequeño que el input sin perder información, ya que al quedarse con los valores más altos reduce la escala de los patrones conservándolos.
Por otro lado, al generar imágenes de los patrones más pequeñas, hace que estas sean más afines a una red neuronal convencional.
Probablemente pienses… ¿Seguro que no se pierde información? Si el output es más pequeño… ¿no estamos bajando la resolución? Para que estés seguro de lo que digo, te muestro un ejemplo:
img_gray = img.convert(‘L’)
img_gray_np = np.array(img_gray)# Función para aplicar max-pooling
def max_pooling(image, kernel_size):
h, w = image.shape
h_pool = h // kernel_size
w_pool = w // kernel_size
pooled_image = np.zeros((h_pool, w_pool))for i in range(h_pool):
for j in range(w_pool):
pooled_image[i, j] = np.max(image[i*kernel_size:(i+1)*kernel_size, j*kernel_size:(j+1)*kernel_size])return pooled_image# Aplica max-pooling con un kernel de 2×2
kernel_size = 2
img_pooled = max_pooling(img_gray_np, kernel_size)# Muestra la imagen original y la imagen con max-pooling aplicado
fig, axes = plt.subplots(1, 2, figsize=(10, 5))axes[0].imshow(img_gray_np, cmap=’gray’)
axes[0].set_title(‘Imagen original’)axes[1].imshow(img_pooled, cmap=’gray’)
axes[1].set_title(‘Imagen con max-pooling aplicado’)plt.show()
Volvamos a analizar la arquitectura de una red neuronal convolucional…
Básicamente lo que haremos es tratar de generar muchas imágenes de detección de patrones pero muy pequeñas para que nuestra red neuronal clásica pueda detectar los patrones. Para ello, iremos alternando entre capas de convolución y de pooling. Básicamente alternamos entre «buscar patrones» y «condensar información encontrada», luego reanudar el ciclo hasta que las imágenes de los patrones sean lo suficientemente pequeñas para ser digeridas por nuestra red convencional o, en casos sencillos, directamente conectar las capas con el output.
Explicadas las CNNS estamos listos para practicar todo lo que hemos aprendido.
Importamos dependencias
from keras.datasets import mnist
from keras import layers, models
from keras.utils import to_categorical
import numpy as np
import matplotlib.pyplot as plt
from keras import regularizers
from keras.callbacks import Callback
import kerastuner as kt
from keras import callbacks
from keras import optimizers
from keras import models
from google.colab import files
!pip install quickdraw
from quickdraw import QuickDrawData
from google.colab import output
import os
import math
from keras.preprocessing.image import ImageDataGenerator
qd_data = QuickDrawData(jit_loading=False, cache_dir=’/content/quickdrawcache’, print_messages=False)
classes = qd_data.drawing_names
!mkdir «/content/Dataset»
!mkdir «/content/Dataset/Train»
!mkdir «/content/Dataset/Test»
imgs_h = 255
max_index = 0
while True:
max_index+=1
try:
qd_data.get_drawing(label, max_index)
except:
break
return max_index
try:
os.mkdir(dirpath)
except:
pass
test_dir_base = «/content/Dataset/Test»
for each_class in classes:
train_dir = f»{train_dir_base}/{each_class.replace(‘ ‘, ‘_’)}»
test_dir = f»{test_dir_base}/{each_class.replace(‘ ‘, ‘_’)}»
create_dir(train_dir)
create_dir(test_dir)
class_data_count = get_class_count(each_class)
train_index = 0
for i in range(math.floor(class_data_count*0.9)):
img = qd_data.get_drawing(each_class, train_index)
filename = f»{each_class.replace(‘ ‘, ‘_’)}_{train_index}.jpg»
img.image.save(f»{train_dir}/{filename}»)
train_index+=1
test_index = 0
for i in range(math.floor(class_data_count*0.9), class_data_count):
img = qd_data.get_drawing(each_class, test_index)
filename = f»{each_class.replace(‘ ‘, ‘_’)}_{test_index}.jpg»
img.image.save(f»{test_dir}/{filename}»)
test_index+=1
Usamos un «data generator» para tener un dataset más grande. Básicamente ésto lo que hace es crear imágenes nuevas a partir del dataset original. Lo hace aplicando transformaciones como zoom, traslación o rotación.
test_datagen = ImageDataGenerator(rescale = 1/255, validation_split = 0.2)
train_dir_base,
target_size = (imgs_w,imgs_h),
batch_size = 128,
class_mode = «categorical»,
color_mode = «grayscale»,
subset = «training»
)val_generator = test_datagen.flow_from_directory(
test_dir_base,
target_size = (imgs_w,imgs_h),
batch_size = 128,
class_mode = «categorical»,
color_mode = «grayscale»,
subset = «validation»
)test_generator = test_datagen.flow_from_directory(
test_dir_base,
target_size = (imgs_w,imgs_h),
batch_size = 128,
class_mode = «categorical»,
color_mode = «grayscale»
)
Paso muy importante, buscamos los hyperparámetros ideales para nuestro modelo.
# numero filtros convoluciones
filters = hp.Choice(‘filters’, values=[32, 64, 128])#numero de neuronas
hp_learning_rate = hp.Choice(‘learning_rate’, values=[1e-2, 1e-3, 1e-4])model = models.Sequential()# convolution layers:
model.add(layers.Conv2D(filters, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5), input_shape=(imgs_w,imgs_h,1))),
model.add(layers.Conv2D(filters, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.MaxPool2D((2,2))),model.add(layers.Conv2D(filters*2, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.Conv2D(filters*2, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.MaxPool2D((2,2))),
model.add(layers.Dropout(0.3)),model.add(layers.Conv2D(filters*4, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.Conv2D(filters*4, (3,3), padding=’same’, activation=»relu», kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.MaxPool2D((2,2))),
model.add(layers.Dropout(0.4)),# capa del input del clasificador:
model.add(layers.Flatten()),#numero de neuronas
#hp_units = hp.Int(«units», min_value = 32, max_value=512, step=32)# hidden layers:
#model.add(layers.Dense(units = hp_units, activation=’relu’, kernel_regularizer=regularizers.l2(1e-5))),
#model.add(layers.Dense(units = hp_units/2, activation=’relu’, kernel_regularizer=regularizers.l2(1e-5))),
model.add(layers.Dropout(0.2)),# output layer
model.add(layers.Dense(len(classes),activation=’softmax’))model.compile(optimizer= optimizers.Adam(learning_rate=hp_learning_rate),
loss=’categorical_crossentropy’,
metrics=[‘accuracy’])return modeltuner = kt.Hyperband(
model_generator,
objective = «val_accuracy»,
max_epochs = 20,
directory = «models»,
project_name = «psm»
)tuner.search(train_generator, epochs = 20, validation_data=val_generator)best_hps = tuner.get_best_hyperparameters(num_trials = 1)[0]print(best_hps)
Por aquí personalizamos un callback que se llamará cada época para detener el entrenamiento si llegamos al 0.99 de accuracy en los datos de validación.
def on_epoch_end(self, epoch, logs = {}):
if logs.get(«val_accuracy») > 0.99:
print(«Model reached 99,9% of accuracy. Stopping training.»)
self.model.stop_training = True
Configuramos el criterio para guardar los pesos del modelo para que se guarde el punto del entrenamiento con mejor accuracy en los datos de validación.
filepath = «model_checkpoints/checkpoint»,
frecuency = «epoch»,
save_weights_only = False,
monitor = «val_accuracy»,
save_best_only = True,
verbose = 1
)
Instanciamos el modelo con los parámetros más eficientes.
Si ya lo tuviéramos guardado, lo gargaríamos del siguiente modo:
Procedemos al entrenamiento:
early_stop_patience = 5
train_history = model.fit(
train_generator,
epochs=train_epochs,
batch_size=128,
validation_data=val_generator,
callbacks = [
checkpoint_save,
#TrainingCallback(),
callbacks.EarlyStopping(monitor = «val_loss», patience=10, mode = «auto»)
]
)
Guardamos el modelo: ¡Qué no se pierda!
files.download(«/content/model_checkpoint.zip»)
Observamos los resultados:
Función para graficar entrenamiento:
def show_train_history(history, show_acc = False):epochs = [i for i in range(len(history.history[«accuracy»]))]
train_acc = history.history[«accuracy»]
train_loss = history.history[«loss»]
val_acc = history.history[«val_accuracy»]
val_loss = history.history[«val_loss»]fig, ax = plt.subplots(1, 2 if show_acc else 1)
fig.set_size_inches(16 if show_acc else 10, 9)if show_acc:
ax[1].plot(epochs, train_acc, «go-«, label = «Train accuracy»)
ax[1].plot(epochs, val_acc, «ro-«, label = «Validation accuracy»)
ax[1].set_title(«Train history Acc»)
ax[1].legend()
ax[1].set_xlabel(«Epochs»)
ax[1].set_ylabel(«Accuracy»)ax[0].plot(epochs, train_loss, «go-«, label = «Train accuracy»)
ax[0].plot(epochs, val_loss, «ro-«, label = «Validation accuracy»)
ax[0].set_title(«Train history Loss»)
ax[0].legend()
ax[0].set_xlabel(«Epochs»)
ax[0].set_ylabel(«Loss»)else:
ax.plot(epochs, train_loss, «go-«, label = «Train accuracy»)
ax.plot(epochs, val_loss, «ro-«, label = «Validation accuracy»)
ax.set_title(«Train history Loss»)
ax.legend()
ax.set_xlabel(«Epochs»)
ax.set_ylabel(«Loss»)plt.show()show_train_history(train_history)
Con esta explicación quedaría concluido el tutorial de las IA, hemos pasado de forma detallada desde cómo funciona hasta cómo crearla, explicando muchos conceptos específicos y mostrando con código ejemplos de cómo funciona de forma interna ¡Espero que os haya sido de utilidad y nos veremos dentro de poco con otros artículos!







