Uso de Matrices para Redes Neuronales

Matrices en las Redes neuronales

En los últimos años, el aprendizaje profundo ha revolucionado la forma en que abordamos problemas complejos en campos como la visualización de datos, el procesamiento del lenguaje natural y la robótica. Sin embargo, detrás de cada modelo de aprendizaje profundo, hay un complejo entramado de matrices y operaciones matemáticas que hacen posible el aprendizaje y la predicción.

En este capítulo del curso “Aprendiendo a trabajar con IA desde 0”, exploraremos la importancia de las matrices y cómo se aprovecha el paralelismo con GPUs y TPUs para hacer que los modelos sean más eficientes y rápidos.

También hablaremos de los optimizadores para descenso de gradientes, haremos varios ejemplos de su implementación de redes neuronales y vamos a ver cómo su elección puede tener un impacto significativo en el éxito y la eficiencia del aprendizaje automático.

Mi misión es hacer que todo esto no suene a chino y abrir camino para que pronto puedas entrenar tu primera red neuronal 🧠✨

Repaso de capítulos anteriores

Este post pertenece a una serie de artículos que forman el curso completo para aprender a trabajar con inteligencia artificial desde cero. Por ello te recomiendo que si no lo has leído, comiences por el primer artículo que te dará las bases para comprender mejor lo que explicaremos en los siguientes

Si no has visto el post anterior te dejamos un enlace aquí donde profundizamos en los siguientes tópicos:

✅ Pendiente
✅ Derivadas y derivadas parciales (sin tablas)
✅ Encontrar el máximo de una función
✅ Descenso del gradiente
✅ Perceptrones
✅ Redes neuronales
✅ Forward Propagation
✅ Backward Propagation

Paralelismo con GPUs y TPUs

Para ello primero quiero hablar de un componente de tu ordenador; la GPU (o Graphics Processor Unit). La GPU (o tarjeta gráfica) es una componente dedicado principalmente al procesamiento de gráficos. La diferencia con la CPU es su capacidad de paralelismo. Imagina que pudieras ejecutar todas las líneas de código de tu programa al mismo tiempo en paralelo. El programa correría muy rápido, ¿verdad? Sin embargo ésto no es posible ya que para que los algoritmos funcionen antes de ejecutar la línea 3 se tiene que ejecutar las lineas 1 y 2. Por ejemplo, si la línea 3 hace uso de una variable modificada por la línea 1 y 2. Por ello las CPUs están diseñadas para ejecutar una cola de instrucciones en orden rápidamente.

Las GPUs, por contrario, son una unidad de procesamiento diseñada para programas que sí pueden paralelizar mucho código a la vez. Cuando se renderiza un modelo 3D en nuestra pantalla, por ejemplo, el código que se ejecuta por cada pixel es el mismo pero con datos de entrada diferentes. Ésto permite mandar a ejecutar las mismas operaciones sobre diferentes datos al mismo tiempo. Cada ejecución no tiene necesidad de esperar a que la ejecución “del pixel vecino” termine. Por ello la estrategia de la GPU es tener un montón de unidades de procesamiento mientras que la CPU es un hardware especializado en programas secuenciales.

Existen algoritmos que permiten realizar cálculos matriciales muy rápidamente desde la GPU sacando partido al paralelismo. Es por ésta razón que las GPUs se utilizan mucho para el machine learning y la ciencia de datos. El entrenamiento de una red neuronal es una tarea de muchas iteraciones.

Las GPU están diseñadas para el procesamiento de gráifcos. Razón por las que se inventaron las TPU (Tensor Processor Unit). Es un concepto similar solo que su arquitectura está optimizada para operar con tensores (dicho mal y pronto, los tensores son matrices anidadas y las veremos en detalle cuando implementemos nuestra primera red profesional). Es un hardware diseñado para redes neuronales.

En python contamos con numpy, una librería que nos permite hacer uso de nuestra GPU/TPU con una sintaxis sencilla para operar sobre conjuntos de datos y realizar operaciones matriciales (entre muchas otras cosas).

Optimizando la red neuronal con matrices

De ahora en adelante quiero que entiendas que todas las fórmulas que hemos hablado y que hablaremos son expresadas mediante operaciones matriciales siempre que sea posible.

Multiplicación de matrices

La multiplicación de matrices consiste en el sumatorio de filas por columnas tal que:

Dada una matriz A y una matriz B cuyo resultado es la matriz C:

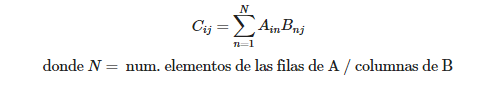
Dicho de una forma algo más gráfica…

No es de mi interés hacer una clase magistral de las matrices. Pero sería recomendable investigar acerca de sus propiedades, operaciones, inversa, determinante…

Ejemplo: Optimizando el forward propagation

Imagina que tenemos una red neuronal de 4 con el siguiente aspecto:

En lugar de usar un bucle for para ejecutar el código del perceptrón de cada neurona, podemos usar una multiplicación de matrices.

Podemos representar los pesos de las neuronas en la que conectan la capa del input con la primera capa oculta en la siguiente matriz:

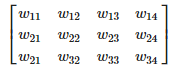
Dejando de lado el bias y la función de activación, podemos realizar la operación de todos los perceptrones del siguiente modo:

¡Hemos logrado expresar la suma ponderada en multiplicación de matriz!

Ahora vamos a introducir el bias en la operación…

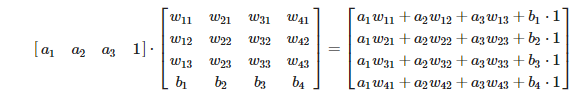
¿Te diste cuenta? Añadiendo un 1 a la matriz que guarda los inputs podemos simular sumar solamente el bias. Y aquí te preguntarás, ¿seguro que esto es eficiente? Estamos computando un total de 4 multiplicaciones innecesarias. Ya que… ¡Para multiplicar por 1 no multiplico nada! La realidad es que el poder del paralelismo y la optimización de multiplicaciones de matrices nos sale más a cuenta.

Pues así va la cosa: Todo lo que podamos expresar en forma de multiplicación de matrices lo hacemos así. Y lo que no, lo mandamos a ejecutar en paralelo (donde cada unidad de procesamiento ejecutará código para un valor de la matriz diferente). En éste caso, si por ejemplo elegimos usar la función de activación “ReLu” la ejecutaríamos en paralelo.

Supongo que ya habrás deducido por qué no hice el código de backpropagation con matrices. Es un concepto sencillo pero que, entre tantas filas y columnas, tiende a confundir a los estudiantes. Por ello suelo posponer explicar esto.

El problema de mínimos locales

Recapitulando, en el pasado documento hablamos de cómo encontrar máximos y mínimos de una función. Ya sea mediante derivadas escaladas de una función o descenso de gradiente.

Observa la función del seno y trata de decir qué valor en x genera el valor en y más grande. ¿Y el más pequeño?

sin(x) function

Pues resulta que el sinus oscila entre 1 y -1, pero hay varias x que nos permiten encontrar esos valores en y.

Ahora observa la misma función pero sumando x al sinus:

sin(x)+.5x function

Si empezamos a ejecutar el descenso del gradiente sobre esta función con un valor inicial de x = 5, el descenso del gradiente convergerá a 5. Sin embargo, existen valores posibles para x que obtendrían mínimos y máximos más extremos.

La solución para éste problema pasa por modificar L (el learning rate). La técnica más común consiste en tener una “agenda de Learning Rate”. Básicamente, después de cierto número de iteraciones sin encontrar un mínimo más pequeño, hacernos nuestro L más pequeño para obtener una x cada vez más precisa. Esto nos permite empezar con una L más grande que nos permitirá ignorar los baches de la función.

Optimizadores

Ok, imagina que estamos entrenando una red neuronal. Para visualizar el entrenamiento, usaré una función multivariable cuyo mínimo se encuentre simplemente aumentando el valor en X e Y. En concreto, para visualizar el problema que quiero enseñarte he planteado una función con perturbaciones en el gradiente que casi provoque mínimos locales.

Función graficada

Si sobre la función planteada aplicamos el descenso del gradiente, iremos haciendo un caminito con forma de “s” mientras “bajamos”.

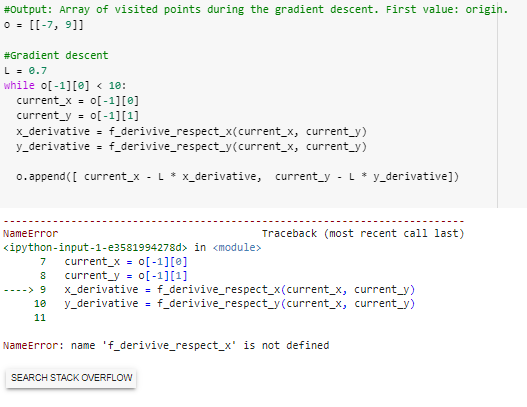
Descenso del gradiente sobre la función

¡Genial! Más o menos va para abajo sin caer en ningún mínimo local. Sin embargo… Esto no es del todo realista si lo queremos plantear como una abstracción del entrenamiento de una red neuronal. Cuando entrenamos una red neuronal, por cada iteración del descenso el gradiente usamos datos en la capa de input diferentes. Podríamos verlo como que cada iteración el gradiente sobre el que nos movemos es ligeramente diferente. Para simular esto repetiremos el proceso añadiendo un pequeño offset aleatorio en las derivadas cada vez que se llame a la función. Hecho esto, volvamos a observar el comportamiento del descenso del gradiente.

Repetimos el descenso del gradiente…

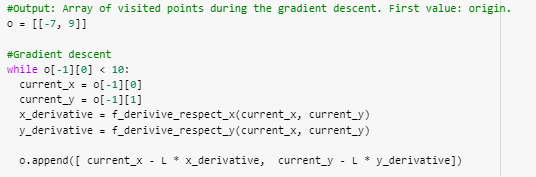
Descenso del gradiente sobre la función con ruido.

¿Te diste cuenta? El camino es mucho más ineficiente. Pues esto pasa cuando entrenas una red neuronal. Imagina que estás entrenando un red para detectar animales. Quizás en una iteración le pasas una foto de un gato y en la siguiente la de un perro o un pangolín. Durante la iteración 1 estás usando “el gradiente para detectar gatos”, durante la segunda, perros. Y durante la tercera, pangolines. Cada iteración sirve a un propósito particular y no al propósito general (detectar animales).

Hay un detalle en descenso del gradiente aplicado a redes neuronales que he omitido por razones didácticas. Y es que antes de aplicar el vector gradiente realiza un promedio de TODOS los gradientes que produce el dataset.

El planteamiento es el siguiente: El problema es que debemos actualizar los parámetros de nuestra red en pro del propósito general y no de cada elemento del dataset con el que entrenamos (cada offset). ¿Solución? Hacer un promedio. Claro que, promediar todo el dataset para un sólo update es demasiado. El número de operaciones se eleva al cuadrado.

Aquí es donde entran en juego los optimizadores. Un optimizador es una técnica para aplicar las derivadas (gradiente) a los parámetros para conseguir un acercamiento a los mínimos locales. En este documento veremos varias alternativas y las compararemos. ¡Comencemos!

SGD: Stochastic gradient descent

Con gradient descent, promediar todo el dataset para un sólo update es demasiado. Por ello tomamos sólo un cierto número de derivadas/gradientes y utilizamos el promedio generado por varios offsets (inputs) en las mismas x e y.

Por ejemplo, hagamos que cada 10 iteraciones se calcula el promedio y se actualizan los parámetros:

SGD sobre la función

A penas sigue igual. Además, el número de iteraciones es mucho mayor. Sin embargo el numero de iteraciones es mucho mejor que si hiciéramos el promedio de un dataset completo. Y es que para una función como la que se presenta en éste caso, es muy fácil quedarse estancado haciendo “s”. Sigamos experimentando con otros métodos más modernos…

Momentum

La técnica momentum viene del concepto de momento de la física. Básicamente en lugar de simplemente aplicar el gradiente a los parámetros, aplicaremos el gradiente a un momento que se aplicará a los parámetros cada iteración. Para conseguir éste efecto el momento se actualiza con una suma ponderada entre el momento y el gradiente que da mayor peso al momento actual.

Éste momento por estándar lo llamaremos v. Y la ponderación se hará mediante β=0.9

Momentum sobre la función

¡Mucho mejor! Pero existen métodos aún más eficientes…

RMSProp

Tal como hemos visto, el comportamiento del momento funciona de forma que, cuanto más grande es la diferencia entre el momento actual y el gradiente de la iteración, mayor impacto tiene el gradiente de la iteración actual. Ésta relación momento-gradiente se comporta de manera lineal. Es decir, la medida en la que la diferencia de magnitud del momento afecta sobre el gradiente es lineal. Tal como podemos visualizar en si graficamos la función f(m,g)=m−(β⋅m+(1−β)⋅g) que nos expresa el diferencial del momento dado un momento anterior y un gradiente.

Graficamos

Ahora, observemos la evolución de un parámetro w al que le aplicamos el momento actualizado cata iteración con un gradiente constante:

Graficamos

Como puedes observar, funciona como una aceleración ya que el momento va “acumulando” fuerza.

La idea detrás de RMSProp es que, si el momento funciona tan bien, exponenciar ese proceso de “acumulación” funcionará mejor. Hace lo mismo que momentum pero el efecto del gradiente sobre el peso y el momento es exponencial. Observa la fórmula:

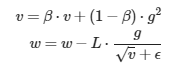
Visualicemos el efecto sobre el peso en función de la magnitud del momento exponenciado y del gradiente de la iteración.

Para ello usaré la función f(x,d)=d/√(βx+(1−β)x)+10−9 donde el parámetro x representa el momento exponenciado y d representa el gradiente hallado en la iteración.

A más magnitud tenga el momento acumulado (eje x, rojo) menor imagen produce el gradiente de la iteración actual (eje y, verde).

Por ejemplo, visualicemos el mismo gráfico con un gradiente constante:

Graficamos

Como ves, la única diferencia entre momentum y RMSProp es que el efecto del momento es exponencial. Veamos cómo funciona.

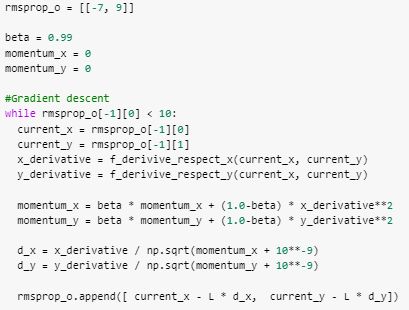
RMSProp sobre la función

¡El número de iteraciones es muy bajo! ¡Excelente!

Adam

El concepto de Adam es tan sencillo como aplicar RMSProp en lugar de sobre el gradiente, sobre el momento.

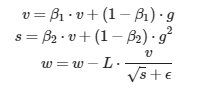
Adam sobre la función

El camino es nítidamente casi recto en la dirección correcto. Magnífico.

Comparativa: graficamos

Ya hemos visto que hay varias opciones para optimizar y debemos buscar la que mejor se ajuste a nuestro modelo, pero incluso con las técnicas más avanzadas de matrices, paralelismo y optimización, hay un problema común que afecta a los modelos de aprendizaje profundo: el sobreajuste u overfitting.

A medida que los modelos se vuelven más complejos y se ajustan mejor a los datos de entrenamiento, pueden perder su capacidad para generalizar y producir resultados precisos en datos nuevos. En el siguiente artículo, exploraremos las causas del sobreajuste y varias técnicas efectivas para prevenirlo o solucionarlo, lo que es fundamental para garantizar el éxito y la eficiencia de las redes neuronales.

¡Hasta la próxima padawans!