Cómo funciona la IA
Si estás aquí porque te has preguntado cómo funciona la inteligencia artificial para tomar decisiones y cómo es posible que aprendan por si solas, has llegado al lugar correcto
¿Te has maravillado al ver cómo los sistemas de inteligencia artificial pueden reconocer imágenes, traducir idiomas y responder preguntas con una precisión sorprendente? Todo esto es posible gracias a las redes neuronales, una de las tecnologías más importantes y revolucionarias en el mundo de la inteligencia artificial.
En este apasionante artículo, exploraremos las redes neuronales y descubriremos cómo funcionan estos sofisticados sistemas.
Guiaré tus primeros pasos a través del mundo de la IA donde aprenderás sobre los conceptos clave, desde la estructura básica de una red neuronal hasta cómo se entrenan para que en el futuro lo apliquemos en la solución de diferentes problemas.
Utilizaremos lo aprendido en el capítulo anterior sobre derivadas, ya que es fundamental para la comprensión de redes neuronales profundas.
Al igual que en el cerebro, las redes neuronales aprenden a partir de la experiencia, y las derivadas son una parte importante de este proceso.
Si no lo has hecho aún, te recomiendo que antes de zambullirte en este capítulo, leas el Tutorial de Inteligencia Artificial. Entendiendo Derivadas que te será de gran utilidad.
Así que, si estás listo para comprender cómo funcionan las máquinas inteligentes y quieres tener una idea de cómo podrían cambiar el mundo en el futuro, este es el artículo perfecto para ti. ¡Al ataque!
Redes neuronales en la IA
Las redes neuronales, como concepto, son algo sencillo de entender. Partimos de la siguiente premia: «Vamos a observar cómo funcionan las estructuras neuronales del cerebro humano para ver si podemos simularla y que sea funcional para resolver tareas».
Al igual que en nuestro cerebro, una red neuronal se define por un conjunto de neuronas conectadas entre sí en una estructura determinada. Bien, pues el primer paso para entender una red neuronal es entender una neurona. En computación llamamos perceptron a la simulación de una neurona.
La rigurosidad sobre el funcionamiento de una neurona orgánica no es del interés de este post así que no seré muy conciso con el proceso biológico además de que no tengo autoridad para hablar de ello.
Si observas la siguiente imagen verás que las neuronas están conectadas entre sí:
Cada neurona recibe el estímulo a través de las dendritas. Cada dendrita es por tanto un canal receptor de estímulos conectado a otra neurona o a uno de nuestros sentidos. Con todos los estímulos recibidos a través de las dendritas la neurona «hace cosas» y genera un estímulo resultante que envía a través de la sinapsis.
Ahora pensemos de manera más técnica.
Sustituye estímulos de entrada por inputs y sinapsis por output y nos queda que una neurona es una cosa que recibe varios inputs y tiene un output. ¡Eso es una función multivariable!
Ok, pero… ¿Qué hace esa función? ¿Cómo se transforman esos estímulos? Se hacen más grandes… más pequeños…? Cada neurona se comporta de manera diferente. Teniendo en cuenta que cada una es diferente podríamos ser creativos y representar una neurona de muchas maneras. Pero el perceptrón es una manera muy cómoda porque es estándar y permite cambiar el comportamiento de la neurona cambiando sus propiedades (lo veremos más adelante).
La simulación de una neurona (perceptrón) se constituye por los siguientes componentes:
- Valores de entrada (x1, x2, x3…)
- Pesos (w1, w2, w3…): Cada valor de entrada tiene un peso asociado. Un peso contiene un numero.
- Sesgo (bias / b)
- Función de activación
- Salida / output (y)
Cada neurona recibe la información de los inputs y a raíz de esa información obtiene un valor al que llamamos activación (output). La activación es el resultado de:
- La suma ponderada de todos los input ponderados por su correspondiente peso.
- A dicho sumatorio, añadirle un sesgo (bias). Este sumatorio sesgado es llamado ‘ z ‘.
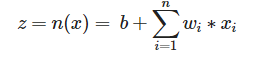
- Evaluar el sumatorio sesgado en la función de activación (llamada ‘ a ‘).
Si te fijas, con éste cálculo si encuentras una combinación de números correcta para los pesos, el bias y usas la función de activación adecuada, puedes simular cualquier comportamiento de transformación de los inputs que puede hacer una neurona.
def activate(weights, bias, inputs): activation = bias for i in range(len(weights)): activation += weights[i] * inputs[i] return activation
En cuanto a las funciones de activación, no le des muchas vueltas a cuál utilizar o por qué unas funcionan mejor que otras. Muchas de ellas se descubren por ‘try and error’. A continuación te muestro algunos ejemplos de funciones de activación.
Sigmoid
La primera en utilizarse. Convierte los valores en un rango de menos infinito a infinito a un rango de 0 a 1.
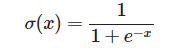
def sigmoid(activation): return 1.0 / (1.0 + exp(-activation))def sigmoid_derivative(output): return output * (1.0 – output) graficate_function(sigmoid, -8, 8, -1, 2)
ReLU
![]()
def reLU(activation): return max(0.0, activation)def reLU_derivative(output): if output < 0: return 0 return 1 graficate_function(reLU, -2, 2, -1, 2)
Tanh
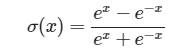
def tanh(activation): return (exp(activation) – exp(-activation)) / (exp(activation) + exp(-activation))def tanh_derivative(output): return 1 – output * output graficate_function(tanh, -8, 8, -1, 2)
Aplicación de las redes neuronales a la IA
La clave de las redes neuronales es que una red neuronal puede solucionar muchos tipos de problema si encontramos una combinación adecuada de:
- Estructura de las conexiones
- Pesos
- Bias
- Funciones de activación
- Un montón cosas que veremos en el futuro…
Del mismo modo que con el descenso del gradiente teníamos una función multivariable y encontrando los ‘ w ‘ correctos podíamos conseguir que el robot mueva el brazo, encontrando los valores correctos podemos hacer que la red neuronal funcione para diferentes tareas.
Hay varios tipos de estructuras de redes neuronales pero la más común es la basada en capa de input, capas ocultas y capa de output.
Cuando nuestra red neuronal recibe un estímulo, este estímulo será retransmitido de neurona a neurona a través de sus conexiones. De momento representaremos las redes neuronales como capas de neuronas conectadas en orden.
De modo que si tenemos 5 capas, la primera tiene cada neurona conectada a todas las capas de la segunda. La segunda, cada una de sus neuronas con cada una de la tercera. Y así con todas las capas. Formando un «circuito complejo de intensidades» que va traspasando de neurona a neurona el impulso transformándolo hasta llegar al final de la red. Éste impulso final, es el resultado de nuestra red neuronal.
Para ser exactos, de todas las capas de la red neuronal, la primera de ellas será la capa del input. La activación de las neuronas de esa capa la escogeremos nosotros en función de la información que queremos procesar. Son la percepción del estímulo que se propaga por la red. La última capa es la que recibe la señal transformada a partir de las intensidades de las conexiones de todas las capas intermedias. Por lo que será el resultado de nuestra red. Y las capas intermedias se les conoce como las hidden layers.
def initialize_network(n_inputs, n_hidden_layers, n_outputs): network = list() for n_hidden in n_hidden_layers: hidden_layer = [{‘weights’:[random() for i in range(n_inputs)], ‘bias’:random(), ‘z’:0.0, ‘delta’:0.0} for i in range(n_hidden)] network.append(hidden_layer) n_inputs = n_hidden output_layer = [{‘weights’:[random() for i in range(n_hidden_layers[-1])], ‘bias’:random(), ‘z’:0.0, ‘delta’:0.0} for i in range(n_outputs)] network.append(output_layer) return network
Generando un dataset random para explicaciones futuras
def load_grades_dataset(size): dataset = list() grades_ponderation = [0.2, 0.15, 0.05, 0.10, 0.3, 0.2] n_grades = len(grades_ponderation) for i in range(size): item = [[random() * 10.0 for g in grades_ponderation], [0.0, 1.0]] grade = 0.0 for i_ponderation in range(n_grades): grade += grades_ponderation[i_ponderation] * item[0][i_ponderation] if grade > 5.0: item[1][0] = 1.0 item[1][1] = 0.0 dataset.append(item) return dataset
Forward propagation
El proceso en el que la capa de Input envía el estímulo a través de la red neuronal es conocido como forward propagation. Es el proceso en el que la red neuronal propaga las señales hasta generar el output.
Generalmente esto se explica incorporando operaciones matriciales en la explicación. ¿Qué significa esto? Los ordenadores son especialmente buenos llevando a cabo operaciones paralelas con matrices así que mucho de lo que voy a explicar requiere conocer álgebra matricial para comprender una implementación de código realista. Yo personalmente discrepo con la mayoría de explicaciones ya que muchos de mis estudiantes vienen sin haber consolidado suficientemente bien los conceptos matriciales. Prefiero explicar los algoritmos SIN matrices (iterativos, no paralelos) ya que son más fáciles de entender. Simplemente ten en cuenta que lo que vamos a explicar a partir de ahora no es la forma de hacer las cosas y haré un documento en el futuro explicando esto más en detalle.
Dicho esto, observemos la siguiente implementación de forward propagation:

def forward_propagate(network, row): inputs = row for layer in network: new_inputs = [] for neuron in layer: activation = activate(neuron[‘weights’], neuron[‘bias’], inputs) neuron[‘z’] = activation neuron[‘output’] = transfer(activation) new_inputs.append(neuron[‘output’]) inputs = new_inputs return inputs
Backward propagation
Ya hemos entendido el concepto de una red neuronal. Ahora nos falta comprender el proceso mediante el cual logramos encontrar la combinación de valores que permite que nuestra red aprenda
Encontrar la estructura de neuronas correcta y saber qué función de activación utilizar es la parte fácil. Pero para eso necesito hablar de algunos conceptos y ¡un solo artículo no alcanza para todo!.
El proceso mediante el cual se obtienen los pesos y bias adecuados para nuestra red es el entrenamiento mediante backward propagation.
La idea es la siguiente:
La red neuronal se inicializa con valores random.
Interpretamos la red neuronal como una función multivariable
Al igual que con el brazo robot, derivamos esa función multivariable y obtenemos para cada parámetro y obtenemos el gradiente que nos permite encontrar los parámetros ideales.
¡Bien, pues vamos allá!
Derivando la red neuronal
Realmente lo que vamos a derivar es la función (C). La función (C) es recibe como parámetro la capa de output de la red neuronal y como resultado escupe «qué tanto se ha equivocado la red». A esto se le conoce como función de coste y hay varios tipos también, si quieres que hablamos de ello… ¡Lo harémos! Solo déjame un comentario para saber que te interesa
De momento usaremos la función de coste más utilizada, que representa la diferencia entre el valor obtenido ‘ o ‘ y el valor esperado ‘ y ‘.
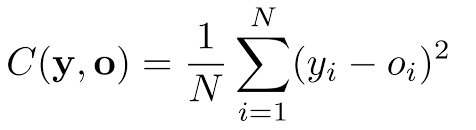
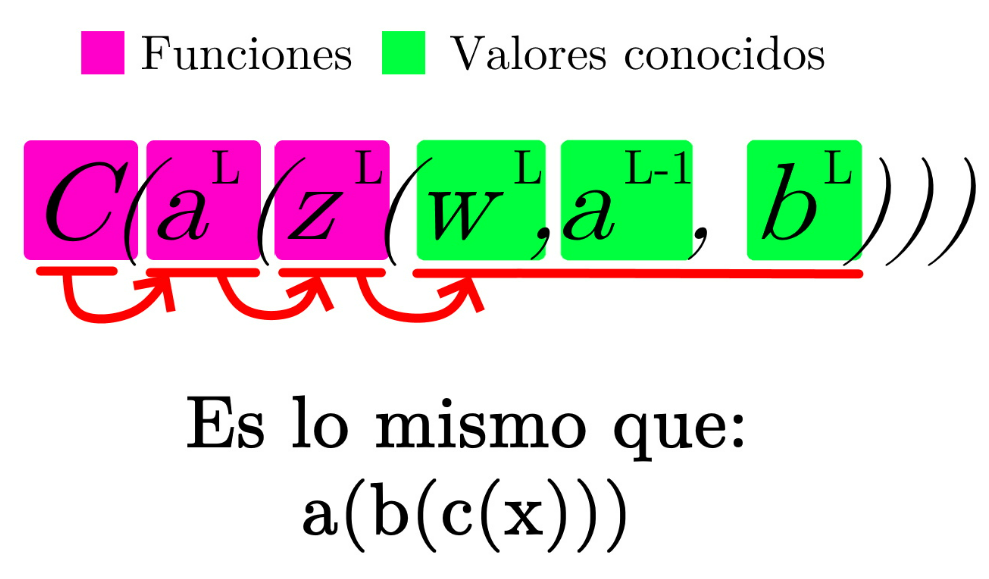
Para una red neuronal de una única capa oculta, la función de coste recibe como parámetro:
![]()
¿Te suena? ¡ES COMO LA PRIMERA DERIVADA QUE APRENDIMOS! Podemos aplicar la regla de la cadena.
Por tanto, para derivar respecto a los pesos ‘ w ‘:
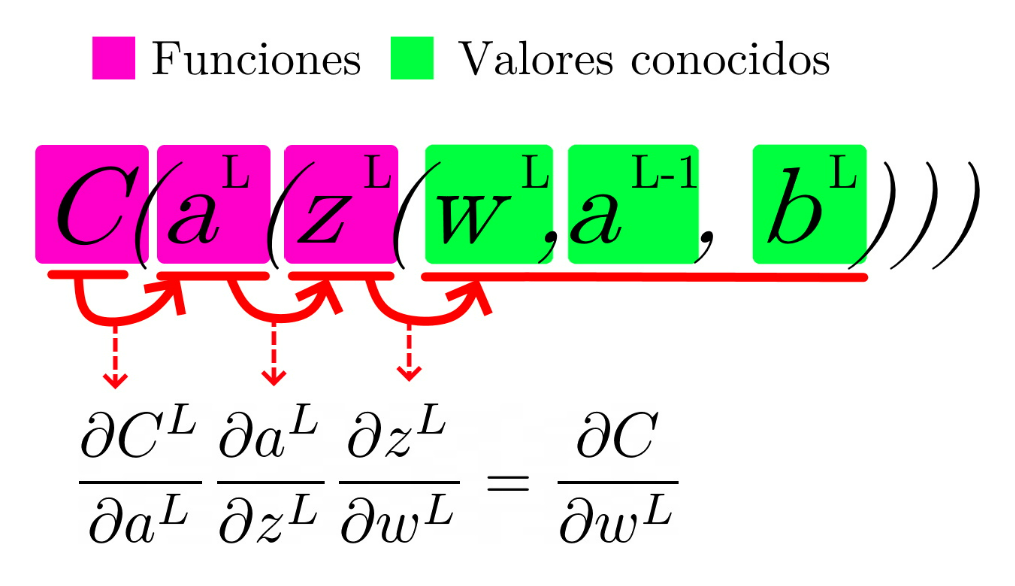
Si te fijas, para derivar respecto al sesgo solo cambia:
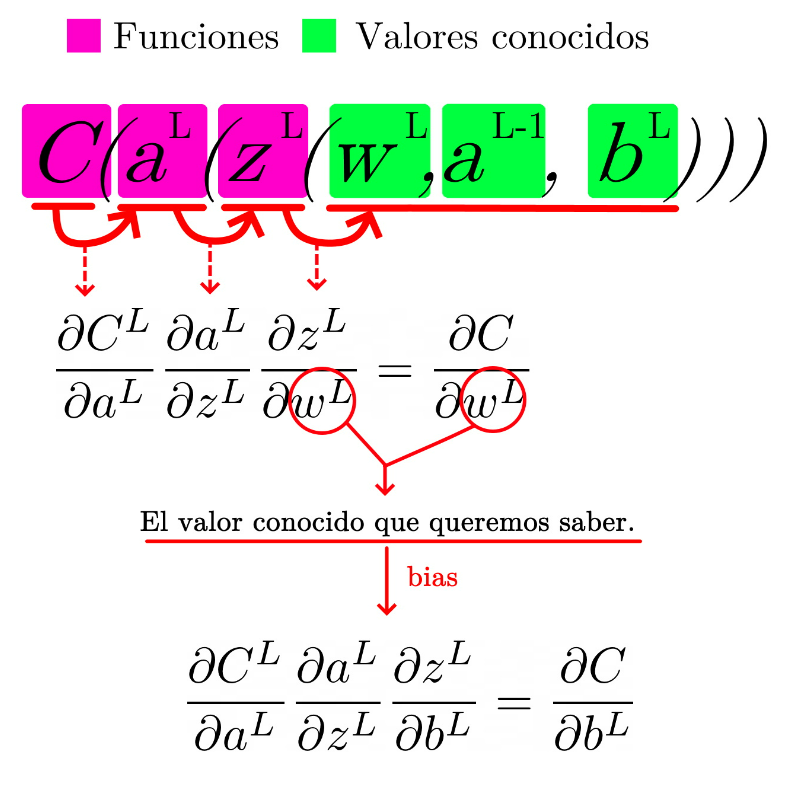
¡Mu’ bien! Ahora vamos a probar con una red de dos capas ocultas:
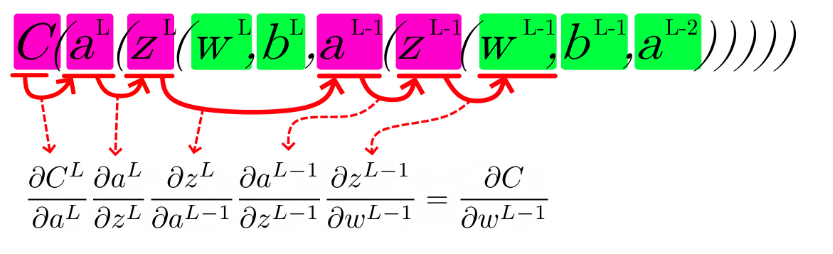
¡Échale más diseño! Veamos cómo queda con 3 capas ocultas:
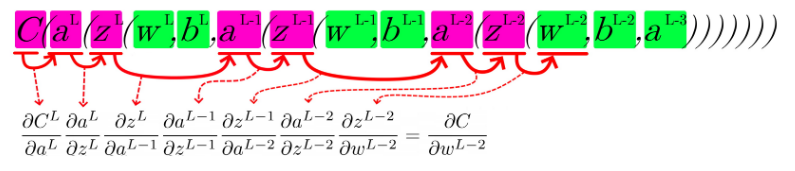
¡Y ahora con 4 capas!
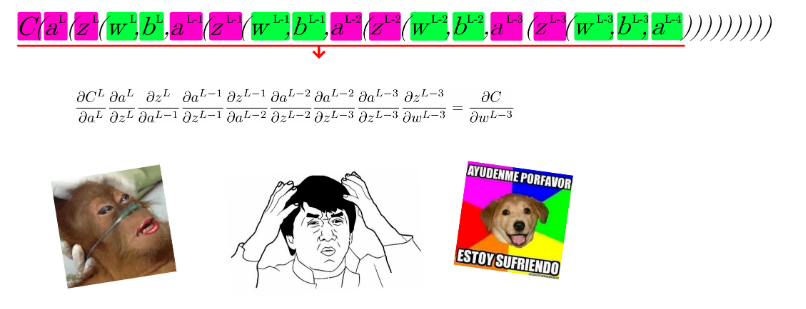
Con 5… Bueno… Alomejor nos estamos complicando la existencia…
Vale, supongo que te habrás dado cuenta de que queda un churro bastante largo e incómodo. Pero de ahí podemos analizar y buscar mejores formas de expresar lo que estamos haciendo. En la siguiente imagen te muestro todas las derivaciones que te acabo de mostrar juntas.
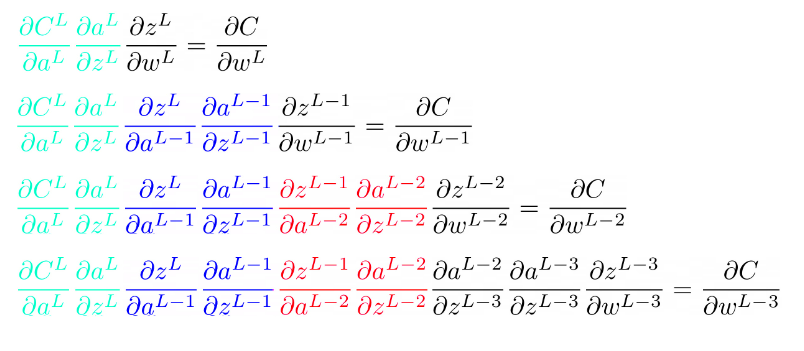
Si te fijas:
La parte referente a la primera capa se repite en todas los casos con una o más capas (color verde).
La parte referente a la segunda capa se repite en todas los casos con dos o más capas (color azul).
La parte referente a la tercra capa se repite en todas los casos con tres o más capas (color rojo).
Como sigue un patrón, podemos simplificar cambiando las derivadas que ya conocemos por un símbolo con el índice de la capa.
Por estándar, este índice se expresa como «L-n» donde L es la última capa.
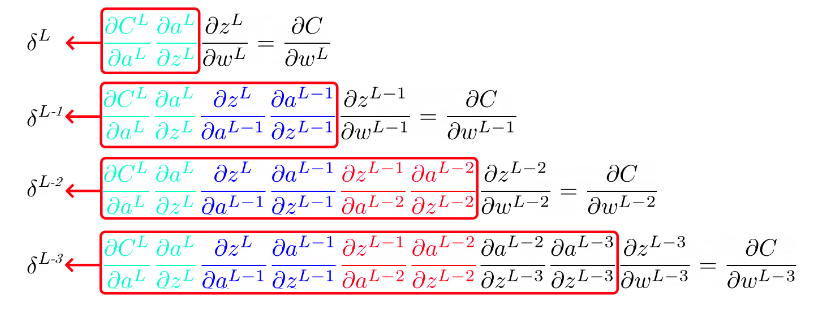
Lo cual se simplifica a:
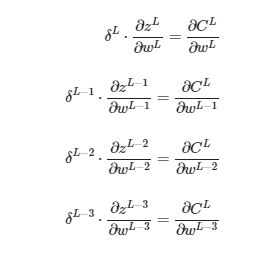
De forma que, expresado de forma general:
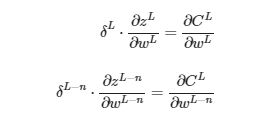
Y si haces las derivadas usando por ejemplo la función sigmoid como función de activación:
Valor del simbolito » δL » para la capa del output:
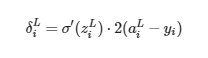
Sin embargo, teniendo en cuenta que más adelante ya estamos multiplicando por un valor arbitrario (el learning rate) multiplicar por una constante no tiene sentido porque es redundante. Por ello a pesar de la derivada eliminamos la multiplicación del 2.
![]()
Para las hidden layers es un poco más complicado. Partamos de la formula y vayamos sustituyendo símbolos/derivadas por sus calculos:
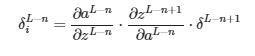
Vamos a empezar por el símbolo δL−n+1. Con este símbolo nos estamos referiendo al δ de la siguiente capa (L-n+1). PERO, dado que en dicha capa cada neurona tiene su propio δ, NO estamos usando UN solo δ y dado que las conexiones están ponderadas no todos tienen la misma importancia. Por ello, tenemos que hacer una suma ponderada usando los pesos que conectan cada neurona con la neurona de la que estamos calculando su δ. Y dado que no queremos que el valor del simbolito dependa del numero de neuronas por capa, lo vamos a promediar.
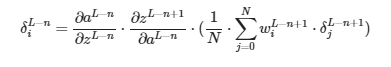
Este es el paso más difícil de entender, tómate tu tiempo. A continuación sustituimos las derivadas por su cálculo:
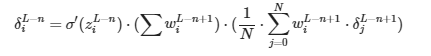
Interesante… Parece que la derivada de ∂zL−n+1/∂aL−n es el sumatorio de los pesos que conectan la siguiente capa con la neurona. Éste sumatorio, a parte de ser una constante como el 2 que ya hemos eliminado hace que los δ sean más grandes o más pequeños en función del número de neuronas por capa. Cosa que no nos interesa. Por ello, siguiendo la misma lógica que con el 2, lo vamos a eliminar de la fórmula.
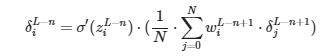
Derivadas parciales de pesos y bias:
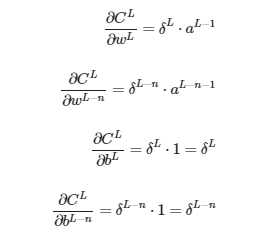
Significado de δL
Vamos a reflexionar un momento. Hasta ahora hemos concebido el símbolo δL como «ese calculo que se repite y me voy guardando para simplificar el proceso».
Pero seamos rigurosos, δ tiene un significado más allá de «el simbolito».
Fíjate de nuevo en la siguiente imagen:
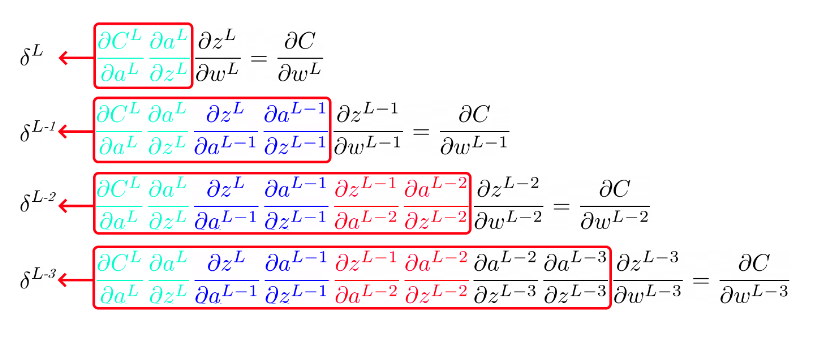
Cada δ es la derivada de del coste de cada capa. Por lo que se conoce como error imputado a la capa L al símbolo δL
Estrategia para calcular el backpropagation
Bien, ahora que ya tenemos las fórmulas en mente, vamos a definir una estrategia para calcular todas las derivadas parciales de todos los pesos y bias. Para simplificar el código, nuestra estrategia va a consistir en calcular únicamente los δ (deltas) de todas las neuronas y luego, cuando tengamos almacenado ese valor haremos el cálculo de las derivadas parciales.
Calculando los deltas
Para mostrar gráficamente el cálculo de los deltas usaremos la siguiente red neuronal como nuestro lienzo en blanco y sobre él iremos «pintando» la información que tengamos en el mismo orden de calculación.
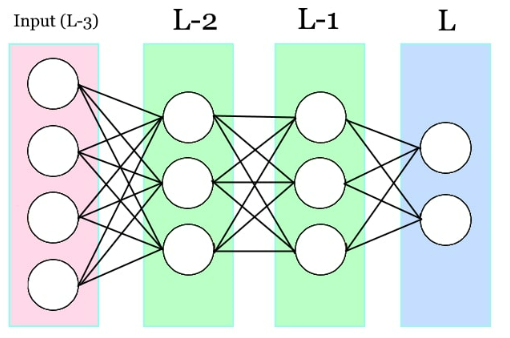
Como era de esperar, antes de realizar ningún cálculo tenemos los pesos y los bias.
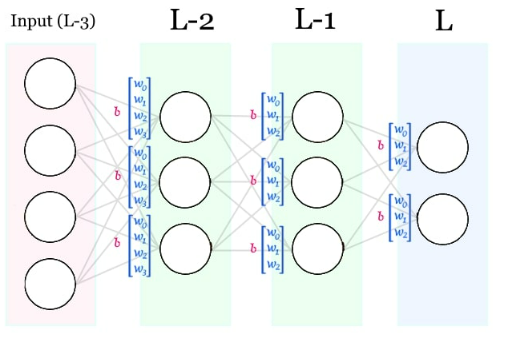
Una vez realizado el forward pass, contaremos con las activaciones y z’s de nuestra red.
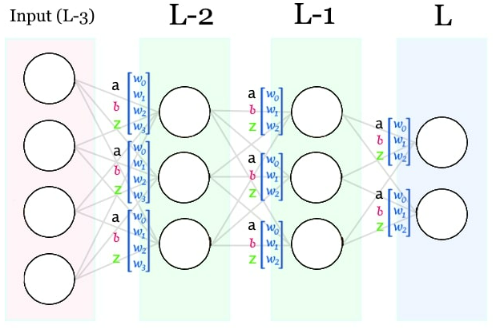
Desde la capa del output, empezamos a calcular sus deltas tal como hemos explicado antes.
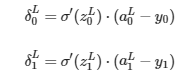
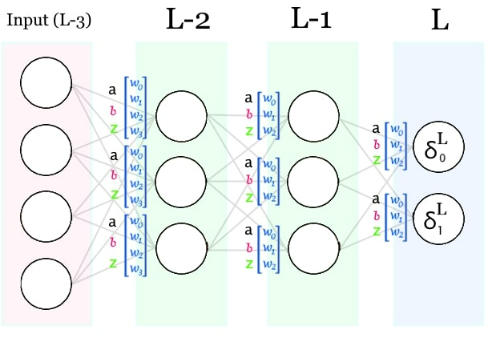
Una vez calculados los δ (deltas) de la capa del output, podemos calcular los de la siguiente capa.
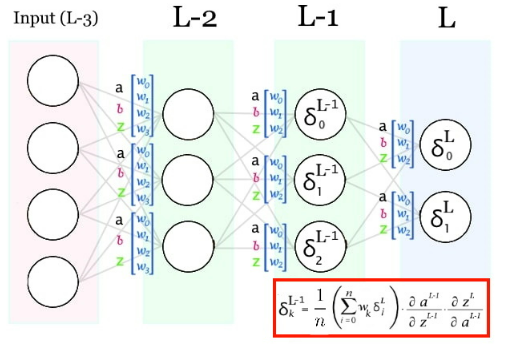
Y entonces los de la siguiente!
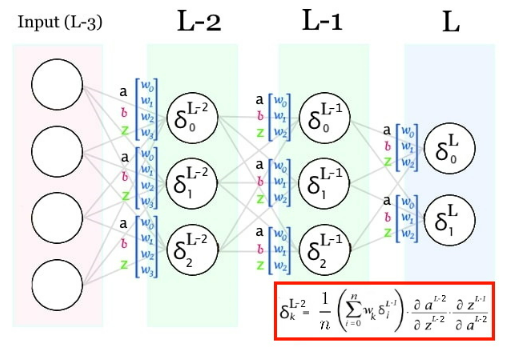
Ahora que ya tenemos los deltas, calculamos el gradiente capa por capa.
Capa del output:
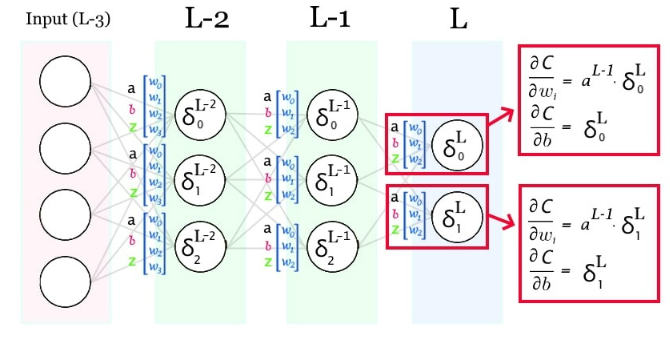
Capa anterior:
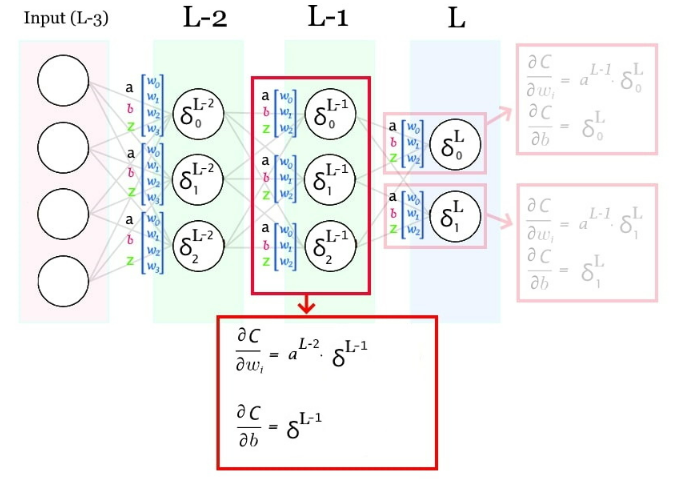
Capa anterior:
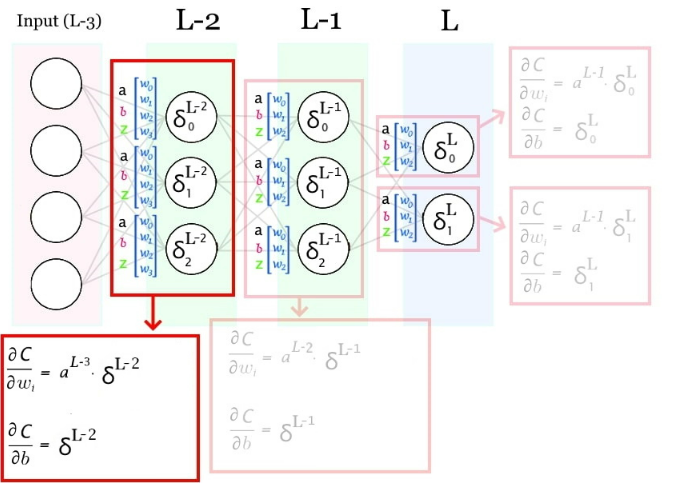
# funcion para simplificar la lectura del algoritmodef is_output_layer(i_layer, len_network): return i_layer == (len_network – 1)transfer = sigmoidtransfer_derivative = sigmoid_derivativetransfer_parameter = ‘output’# Backpropagate error and store in neuronsdef backward_propagate_error(network, expected): for i_layer in reversed(range(len(network))): layer = network[i_layer] for i_neuron, neuron in enumerate(layer): if is_output_layer(i_layer, len(network)): neuron[‘delta’] = transfer_derivative(neuron[transfer_parameter]) * (neuron[‘output’] – expected[i_neuron]) else: delta_Lplus1 = sum([next_n[‘weights’][i_neuron] * next_n[‘delta’] for next_n in network[i_layer + 1]]) / len(network[i_layer + 1]) neuron[‘delta’] = transfer_derivative(neuron[transfer_parameter]) * delta_Lplus1
Obteniendo y aplicando el gradiente
def update_weights(network, row, l_rate):
inputs = row[:]
for i in range(len(network)):
if i != 0:
inputs = [neuron[‘output’] for neuron in network[i – 1]]
for neuron in network[i]:
for j in range(len(inputs)):
neuron[‘weights’][j] -= l_rate * neuron[‘delta’] * inputs[j]
neuron[‘bias’] -= l_rate * neuron[‘delta’]
Entrenando la Inteligencia Artificial
def train_iteration(network, train_dataset, l_rate): sum_error = 0 for i, row in enumerate(train_dataset): # forward progagation outputs = forward_propagate(network, row[0]) # format expected output expected = row[1] # calculate error and backward propagate sum_error += sum([(expected[i] – outputs[i]) ** 2 for i in range(len(expected))]) backward_propagate_error(network, expected) # apply gradient descent update_weights(network, row[0], l_rate) # return the error avg return sum_error / len(train_dataset)# Train a network for a fixed number of epochsdef train_network(network, train_dataset, l_rate, n_epoch:int): tracked_info = list() for epoch in range(n_epoch): error = train_iteration(network, train_dataset, l_rate) tracked_info.append({‘error’:error, ‘learning_rate’:l_rate}) return tracked_infodataset = load_grades_dataset(10000)n_inputs = len(dataset[0][0])n_outputs = len(dataset[0][1])n_hidden_layers = [10]lr = 0.04network = initialize_network(n_inputs, n_hidden_layers, n_outputs)training_tracked_info = train_network(network, dataset, lr, 100)errors = [info[‘error’] for info in training_tracked_info]graficate_values(errors, 0, len(training_tracked_info), 0,max(errors), «epoch», «Given error»)
Esto es sólo el comienzo…
Bueno, yo creo que para un primer paso está bien. Pero faltan muchas cosas por comprender con una visión profunda el funcionamiento de las inteligencias artificiales que nos rodean.
Antes te comenté que una red neuronal es una configuración de diferentes aspectos de la red. Bien pues la lista completa es la siguiente:
Estructura de la red: num. Inputs, num. hiden Layers, num. neuronas por capas, num. outputs, conexions.
Learning Rate del descenso del gradiente (puede ser adaptativo).
Funciones de activación.
Estrategia de entrenamiento
Dropout (si lo usa o no, en qué capas, configuración)
Optimizadores (RMSProp, Adam, momentum)
Función de coste elegida
Regularizador
Luego hay más temas avanzados como comprender qué es una CNN, qué tecnologías existen en el mercado, comprender lo que comentamos de expresar las operaciones en forma matricial… para, para
En definitiva. Nos queda mucho por comentar en futuras publicaciones