En este tutorial de Inteligencia Artificial con derivadas, entenderemos el corazón de las redes neuronales y los mecanismos más intrínsecos que las capacitan para aprender a hacer una tarea de forma efectiva. Para el final de este tutorial de Inteligencia Artificial, sabrás programar una simulación de un brazo robot 😱😱😱.
En el campo de la IA, empezar con un propósito claro, simplificará el proceso de ir encajando los engranajes necesarios para que todo lo que te propongas se materialice, desde devolverle a una persona la capacidad de andar, ver, trabajar, hasta reducir los daños ambientales producidos por procesos industriales. ¡Las posibilidades de crear un impacto positivo con inteligencia artificial son infinitas!.
Si necesitas inspirarte con proyectos de software “made in spain” que ya están creando impacto en la sociedad puedes visitar este artículo.
Este es el primero de una serie de artículos para aprender sobre Inteligencia Artificial de forma práctica, te recomiendo seguirnos en el blog para no perderte las próximas publicaciones, y así, avanzar con pie firme por este apasionante campo.
Los primeros pasos en este mundo, vamos a darlos comenzando por las derivadas que serán la clave para iluminar la caja negra de la IA y las Redes Neuronales.
¡Vamos a ello!
[powerkit_toc title=»Table of Contents» depth=»2″ min_count=»4″ min_characters=»1000″ btn_hide=»false» default_state=»expanded»]
Derivadas
Una derivada es una función que expresa la medida de cambio de otra función. Conceptualmente se puede interpretar como la pendiente en un punto determinado de esa otra función. ¡Entonces será tán sencillo como aplicar la fórmula de la pendiente en un punto muy concreto! ¿No? Bueno, la fórmula de la pendiente de la recta requiere de dos puntos y nosotros queremos la pendiente de un único punto.
Por esa razón lo que hacemos para calcular la derivada a partir de dos puntos de la curva muy cercanos. Pero para que esto sirva, esos puntos tienen que estar muy muy pero MUY cerca, sin llegar a tocarse.
Pendiente de la recta:
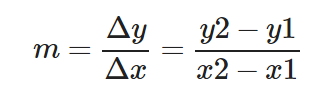
Δy y Δx significan «delta y» y «delta x» respectivamente. Básicamente expresan la magnitud entre dos valores en el eje y/x respectivamente.
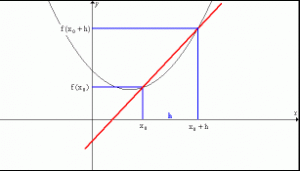
La idea de una derivada es muy sencilla. Si estamos calculando la pendiente entre 2 x muy próximos, obtendríamos la derivada. Por ello decimos que la derivada es la pendiente entre f(x) y f(x+Δx). Donde Δx es un pequeño offset muy pequeño al que generalmente nos referiremos como h. Asumimos que es un valor muy muy pequeño que tiende a 0.
Si no sabes qué es un límite o que algo tienda a 0 te suena extraño visita este video.
Por tanto partiendo de la definición de la pendiente:
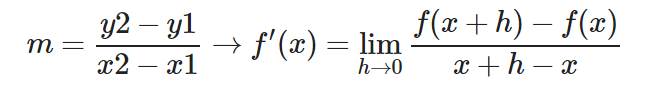
Obtenemos la definición formal de la derivada:
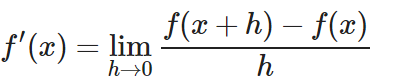
Derivadas parciales
Las derivadas parciales son las derivadas de funciones multivariables (con más de un parámetro). Básicamente, consiste en tomar como constante todos los parámetros menos uno y sumar h a ese parámetro. Básicamente son derivadas normales con un nombre fancy. Al hacer que el resto de parámetros sean constantes es como si la función fuera de un sólo parámetro como el ejemplo anterior.
Para que te familiarices con la nomenclatura, observemos una derivada parcial con 2 parametros (‘y’ se trata como constante para obtener la derivada parcial respecto a ‘x’)
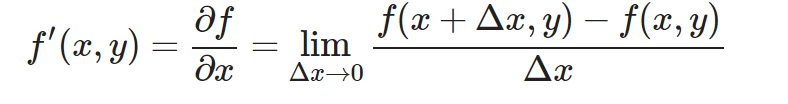
Para que no te suene extraño…
![]() significa «derivada parcial de la función f respecto a x»
significa «derivada parcial de la función f respecto a x»
Proceso de derivación
Probablemente la forma en la que calculas las derivadas es muy diferente a lo que acabas de aprender. Seguramente te hayan enseñado que cuando se cumplen unas condiciones, la derivada de una función es lo que dice una tabla.
Bueno, esto es cierto. Pero es importante tener en cuenta que el origen de cada una de las posibilidades de las reglas de derivación son fruto de:
- Agarrar la expresión formal de la derivada que hemos visto antes.
- Sustituir función (f) por las operaciones que contiene la función.
- «Jugar» con la ecuación hasta eliminar todas las h de la expresión.
- Simplificaremos le ecuación al máximo.
Ahora bien, este proceso está genial para entender de dónde salen las cosas y no conceptualizarlas como cajas negras, donde no se sabe bien qué es lo que se hace. En este post haré alguna derivación como ejemplo pero no necesitas aprender a derivar para entrar al campo de Deep Learning. De hecho, a día de hoy incluso se usan herramientas que derivan cualquier función por ti, sin tablas:
Herramienta gratuita para calcular derivadas
Herramienta gratuita para calcular Derivadas Parciales
Otros recursos interesantes:
Desarrollo teórico de derivadas recomendado (Parte 1)
Desarrollo teórico de derivadas recomendado (Parte2 )
Ejemplo de derivación – Regla de la cadena
Recomiendo que si no has derivado nunca sin tablas mires los enlaces de desarrollo teórico que he compartido arriba. Allí se hacen varios ejemplos. Las reglas que aparecen en la tabla de derivación son muchas y podríamos estar horas demostrando cada una de ellas. Para este documento he escogido la regla de la cadena ya que es el corazón donde se originan las fórmulas que conforman las redes neuronales.
![]()
Se trata de una función (f) cuya imagen (y) es el resultado de una función (k) evaluando el resultado de otra función (g) con ‘x’ como término independiente (parámetro).
¡Muy bien! Pues vamos a intentar encontrar una forma general de derivar una función que llama a otra, que aplique para todos los casos.
f′(x)=?
Como siempre, partiremos de la definición formal de la derivada.
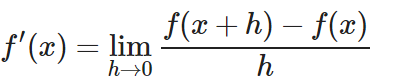
Vamos a aplicar la definición formal a nuestra función (sustituir todos los «f(…)» por las operciones de (f):
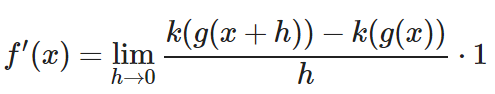
Para el siguiente paso empezaremos a jugar con algebra y a cambiar cosas en la ecuación. Eso sí, cada vez que hagamos un cambio la igualdad se debe respetar. Es decir, la ecuación debe expresar lo mismo en un lado y en el otro. Por ejemplo, no podemos mágicamente sumar un número arbitrario a la derecha del ‘=’.
Nuestra jugada será multiplicar por 1. Justo así:
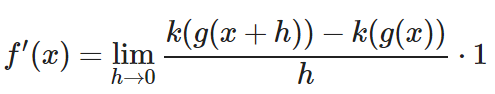
Ya sé, ¡¿Y eso pa’qué?! Este es un truco muy común ya que «1» se puede expresar de muchas formas. Por ejemplo, en fracción. Cualquier número dividido por sí mismo es 1. Por lo que podemos multiplicar por una fracción que tenga numerador y denominador que nos permitan jugar con la ecuación siempre que tengan el mismo valor.
En este caso usaremos lo siguiente:
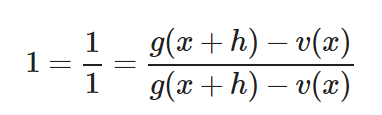
¿Por qué? Bueno, hemos elegido esta fracción pensando en cual nos puede permitir jugar con los números. Veamos cómo queda si multiplicamos nuestra derivada por esta fracción.
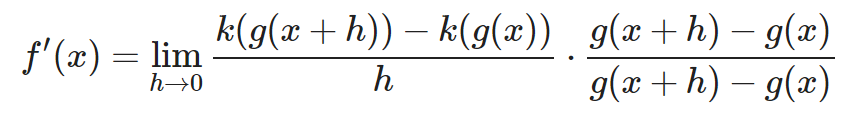
Lo cual es lo mismo que:
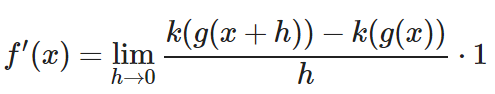
Y por tanto expresa el mismo resultado. Pero… ¡Vaya! Al ser una multiplicación de fracciones, podemos cambiar de lado el numerador/denominador sin alterar el producto.
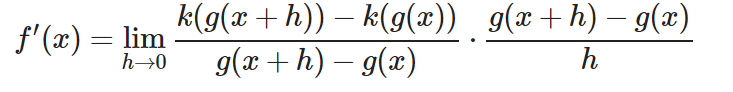
Solamente con esto ya hemos dado un paso muy importante. Fíjate bien en la parte derecha de la multiplicación. ¡Es la expresión formal de la derivada de g!
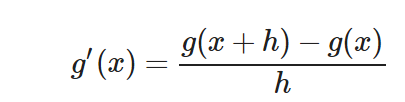
Por ende podemos expresarlo como g′(x) y eliminar esa fracción. Otra forma común sería en lugar de g′(x) usar la notación dg/dx
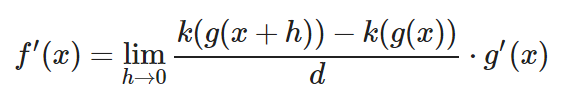
Muy bien, nuestro próximo objetivo es la fracción de la izquierda. Vamos a atacarla empezando por su denominador. Obsérvalo bien:
g(x+h)−g(x)
Si h fuera 0, nos quedaría g(x)-g(x) = 0. Por tanto, podemos deducir que nuestro denominador tiende a 0. Es un número muy muy cercano a 0 que no es igual a h. Por tanto, podemos crear una variable nueva para expresar el denominador con una variable que tiende a 0. En este caso le llamaré ‘ d ‘.
d=g(x+h)−g(x)
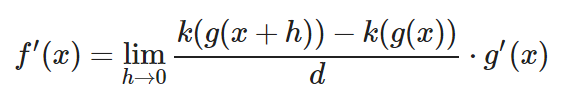
![]()
Ahora ataquemos al numerador. ¿Cómo? Volvamos a observar el valor de ‘ d ‘:
d=g(x+h)−g(x)
Esto no deja de ser una ecuación, de modo que puedo mover cosas de un lado a otro. Observa lo que sucede si movemos g(x) al otro lado:
g(x)+d=g(x+h)
¿Te diste cuenta? Si sustituimos todos los «g(x + h)» por «g(x) + d» en el numerador nos quedaría del siguiente modo:
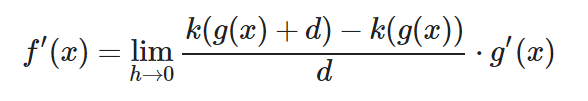
¡LO TENEMOS! Ahora la fracción de la izquierda es la expresión formal de la derivada de (k). Y podemos sustituir la fracción por k'(g(x))
f′(x)=k′(g(x))⋅g′(x)
Para terminar de derivar la función f nos faltaría derivar k y g. Pero si te fijas, acabamos de demostrar que para toda función que consista en funciones anidadas su derivada es la multiplicación de la derivada de cada función anidada.
Y esto se extrapola a infinitas funciones anidadas. Si te paras a ver el resultado pensando en ‘x’ como una función anidada adicional te darás cuenta.
f′(x)=k′(g(z(x)))⋅g′(z(x))⋅z′(x)
Derivadas para encontrar máximos de una función
Visualiza lo siguiente: Si calculamos la derivada de una función en un punto ‘ x ‘ y luego evaluamos esa función en ‘ x ‘ + la derivada en ‘ x ‘ escalada a un número muy pequeño (llamémoslo ‘ h ‘), la imagen será mayor al primer resultado.
f(x)≲f(x+f′(x)∗h)
Esto se debe a que si la derivada es positiva significa que la función está creciendo, por lo que ir hacia delante (incrementar ‘ x ‘) hará que la imagen crezca. Por contrario, si la derivada es negativa, significa que para que la imagen «crezca» debemos decrementar ‘ x ‘ (‘ x ‘ + una derivada negativa).
El único caso donde esto podría no cumplirse es si la función es muy cambiante y Δx es suficiente para provocar un cambio brusco de la derivada. Pero es un caso sumamente improbable.
def f(x):
return x**2*-1
def f_derivative(x):
return -2*x
x1 = 5
y1 = f(x1)
scalar = 0.2
x2 = x1 + f_derivative(x1) * scalar
y2 = f(x2)
x = np.linspace(0,10);
y = f(x);
plt.figure(figsize=(5,5))
plt.plot(x,y)
plt.grid()
plt.plot(x1, y1, marker=»o», markersize=6, markeredgecolor=»red», markerfacecolor=»red»)
plt.plot(x2, y2, marker=»o», markersize=6, markeredgecolor=»green», markerfacecolor=»green»)
plt.text(x1+.5, y1+.5, «f(x)»)
plt.text(x2+.5, y2+.5, «f(x + f'(x)·h)»)
plt.show()
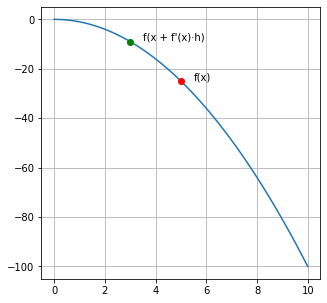
Puedes probarlo con la función que quieras, si encuentras una ‘ h ‘ los suficientemente pequeña la regla siempre se cumplirá.
A partir de éste principio se fundamenta el descenso del gradiente.
Descenso del gradiente
El descenso del gradiente es básicamente hacer lo mismo que he explicado en el apartado anterior pero con una función multivariable para encontrar el punto más bajo o alto de una función. Si repetimos la acción con el ejemplo del apartado anterior muchas veces donde cada vez actualizamos el valor de ‘ x ‘ por ‘ x+f'(x)·h ‘, eventualmente ‘ x ‘ será el parámetro para la función (f) que encuentra el valor más alto.
Partamos de un ejemplo sencillo. En el siguiente ejemplo vamos a generar una superficie mediante una función multivariable simple:
f(x,y)=x2+y2
Lo cual nos genera la siguiente superficie:
fig, ax = plt.subplots(subplot_kw={«projection«: «3d«})
def f(x,y):
return x**2 + y**2;
res = 100
X = np.linspace(-10, 10, res)
Y = np.linspace(-10, 10, res)
X, Y = np.meshgrid(X, Y)
Z = f(X,Y)
# Gráficar la superficie
surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0, antialiased=False)
fig.colorbar(surf)
fig.set_size_inches(18.5, 10.5)
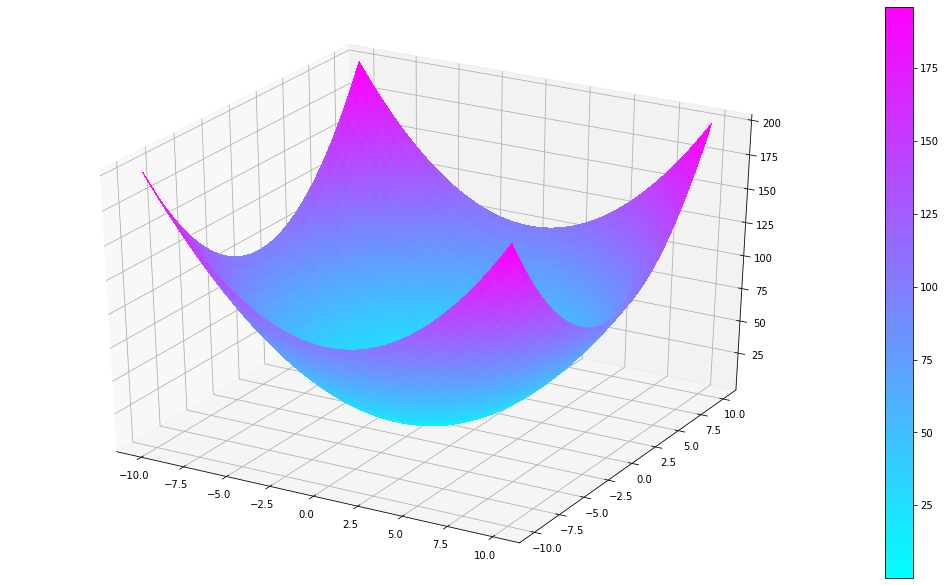
Cuando hablamos de «el gradiente» hablamos de una entidad que almacena todas las derivadas parciales de una función multivariable.
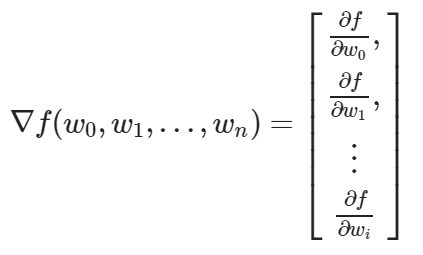
El descenso del gradiente en sí, es un proceso iterativo que nos permite encontrar los mínimos locales de una función multivariable haciendo uso de las derivadas parciales como en el ejemplo de la función mono-variable.
Tal como hemos visto anteriormente, dado un parámetro ‘ w ‘, evaluar la función con la suma de ‘ w ‘ y la derivada de la función en ‘ w ‘ multiplicada por un escalar pequeño nos permite encontrar una imagen más alta. Por tanto, hacer la resta nos permitirá encontrar una imagen más pequeña. Y este es el núcleo del descenso del gradiente.
Ésta vez llamaremos ‘ L ‘ (learning rate) al «escalar pequeño» (antes lo llamábamos ‘ h ‘) por seguir la nomenclatura/notación de las fórmulas.
wi=wi−L⋅∇f(wi,…)

Minimizar errores con descenso del gradiente
El descenso del gradiente por tanto es un mecanismo idóneo para encontrar parámetros que presenten el mejor resultado de una función.
Imagina que tienes un brazo robot y te han pedido que calcules qué rotación debe tener cada junta para que la mano del robot esté lo más cerca posible a un punto concreto del espacio. Esto teniendo en cuenta que estas solo pueden girar en un eje.
Si el brazo robot tiene 4 juntas, nuestra función para aplicar la rotación recibe 4 parámetros (4 ángulos). No debería ser muy difícil generar una función que obtenga la distancia entre la mano y el punto deseado después de aplicar las rotaciones.
d(w0,w1,w1,w1)
Esta función tendrá un resultado más grande cuanto peor resultado tengan los parámetros y más cercano a 0 cuanto mejor funcionen para cumplir nuestro objetivo. Formalmente, llamaremos (d) a nuestra función de coste. Que es la función que nos permite evaluar numéricamente el error generado por los parámetros respecto a nuestro objetivo.
Aplicando el descenso del gradiente sobre esa función podemos encontrar una rotación que minimice la distancia entre la mano del robot y el punto objetivo.
Recodemos que el gradiente estará formado por las derivadas parciales respecto a cada parámetro. Las cuales, siguiendo la definición formal de la derivada (sin simplificar con las tablas) serían:
![]()
De tal modo que para cada parámetro el proceso queda tal que así:
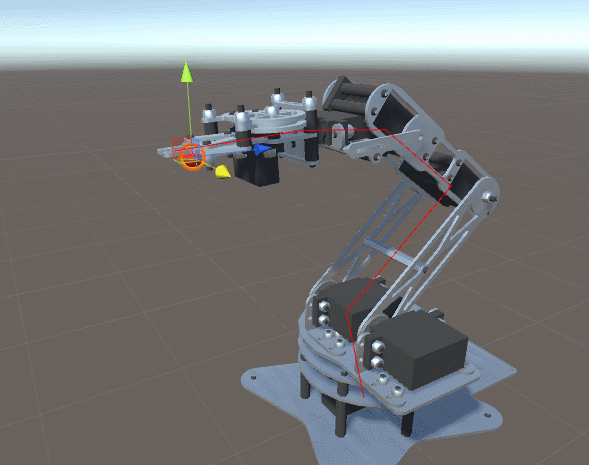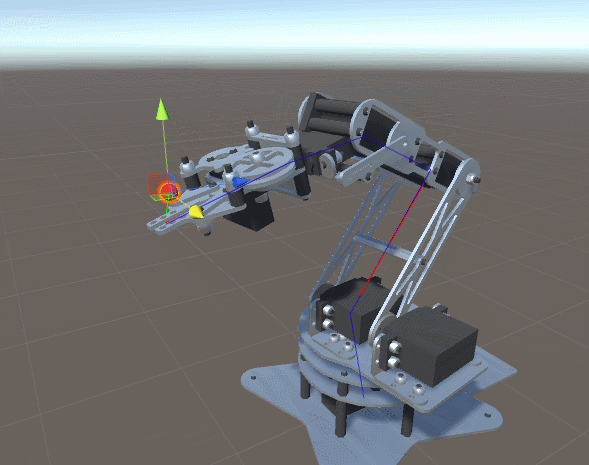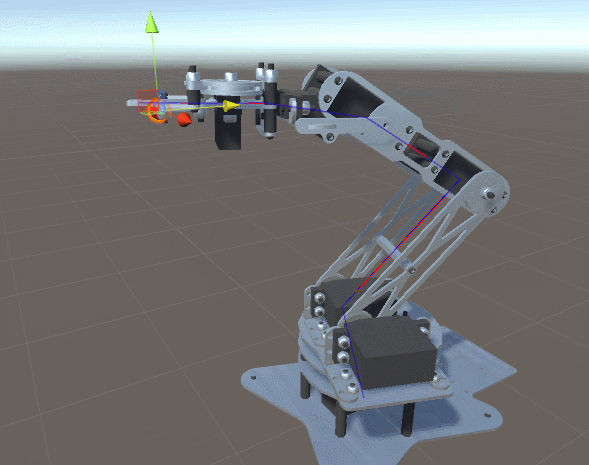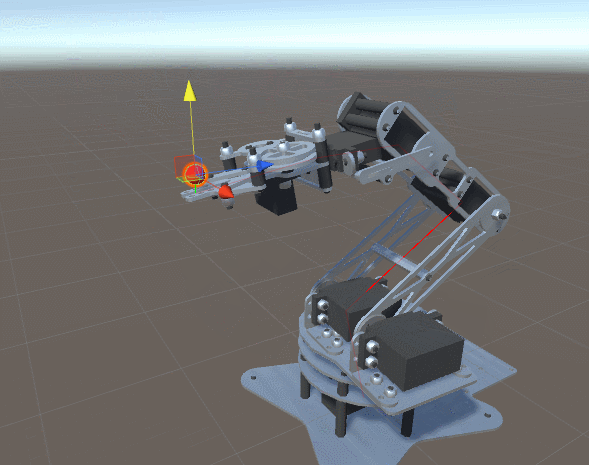
¡Prueba este proyecto en Unity! 🤩
En el siguiente proyecto de unity puedes ver el código fuente que permite realizar el cálculo de las rotaciones mencionado anteriormente.
En próximos artículos hablaremos de las redes neuronales, como se componen y cómo logran aprender tareas complejas. Al igual que en el cerebro, las redes neuronales aprenden a partir de la experiencia, y las derivadas son una parte importante de este proceso. 👀
Esperamos que nos acompañes en este recorrido tan extenso y apasionante. ¡Esto es solo el comienzo! 🚀